Với phân tử Octatetraene, hãy xác định số sóng (cm-1) của ánh sáng cần thiết để kích thích 1 electron từ mức năng lượng cao nhất có electron (HOMO) lên mức năng lượng thấp nhất không có electron (LUMO).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
21 tháng 8 2019
+ Vận tốc của electron khi nó chuyển động trên quỹ đạo thứ n: v ~ 1 n
→ Động năng giảm 9 lần → v giảm 3 lần → n = 6.
+ Bước sóng dài nhất ứng với sự chuyển mức năng lượng từ E6 về E5, bước sóng nhìn thấy ngắn nhất ứng với sự chuyển mức năng lượng từ E6 về E2.
22 tháng 7 2023
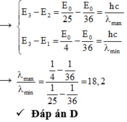
\(\lambda_{max}=\dfrac{hc}{13,6\left(\dfrac{1}{1}-\dfrac{1}{2^2}\right)eV\cdot1,602\cdot10^{-19}J\cdot eV^{-1}}m\cdot10^9nm\cdot m^{-1}=121,56nm\\ \lambda_{min}=\dfrac{hc}{13,6\left(\dfrac{1}{1}-\dfrac{1}{n_{\infty}^2}\right)eV\cdot1,602\cdot10^{-19}J\cdot eV^{-1}}m\cdot10^9nm\cdot m^{-1}=91,17nm\)
TP
4 tháng 8 2021
Cấu hình electron của nguyên tử S (Z=16) : \(1s^22s^22p^63s^23p^4\)
a) Nguyên tử lưu huỳnh có 3 lớp electron
+ Lớp thứ nhất : 2e
+ Lớp thứ hai : 8e
+ Lớp thứ 3 : 6e
b) Phân lớp cuối cùng chứa mức năng lượng cao nhất : 3p
Cấu trúc phân tử octatetraene:
Phân tử gồm bốn cặp electron pi, chiếm các mức năng lượng E1 đến E4 (HOMO).
Từ công thức: \(\Delta E=\dfrac{h^2}{8ma^2}\left(n'^2-n^2\right)\)
suy ra:
\(\Delta E=\dfrac{h^2}{8m_{electron}\left(\left(8+1\right)\cdot\left(1,4\cdot10^{-10}\right)\right)^2}\left(5^2-4^2\right)=3,4\cdot10^{-19}J\\ \overset{-}{\nu}=\dfrac{\Delta E}{hc}=1,7\cdot10^6m^{-1}=1,7\cdot10^4cm^{-1}\)