Tính thể tích của khối chóp cụt lục giác đều \(ABCDEF.{\rm{ }}A'B'C'D'E'F'\) với \(O\) và \(O'\) là tâm hai đáy, cạnh đáy lớn và đáy nhỏ lần lượt là \(a\) và \(\frac{a}{2},OO' = a\).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án D
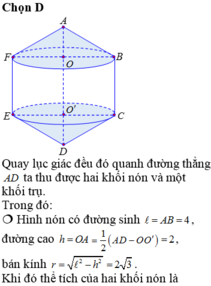
Khi quay lục giác đều đã cho quanh AD ta được 2 hình nón và 1 hình trụ
Hình trục có chiều cao h = B C = 4.
Bán kính đáy r = B H = 4 3 2 = 2 3 .
Hình nón có chiều cao h ' = A H = 2 , bán kính đáy r = B H = 2 3 ; V = π r 2 h + 2 3 π r 2 h ' = 64 π

Đáp án D
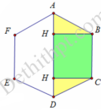
Khi quay lục giác đã cho quanh AD ta được 2 hình nón và một hình trụ
Hình trụ có chiều cao h = B C = 4 và bán kính đáy r = B H = 4 3 2 = 2 3
Hình nón có chiều cao h ' = A H = 2 và bán kính đáy r = B H = 2 3
Khi đó V = π r 2 h + 2 3 π r 2 h ' = 64 π .


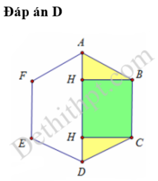

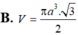
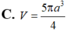
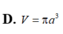
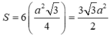
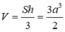
Diện tích đáy lớn của khối chóp cụt lục giác đều:
$[ S = \frac{3\sqrt{3}}{2} \cdot a^2 ]$
Thể tích của khối chóp cụt:
$[ V = \frac{1}{3} \cdot S \cdot h ]$