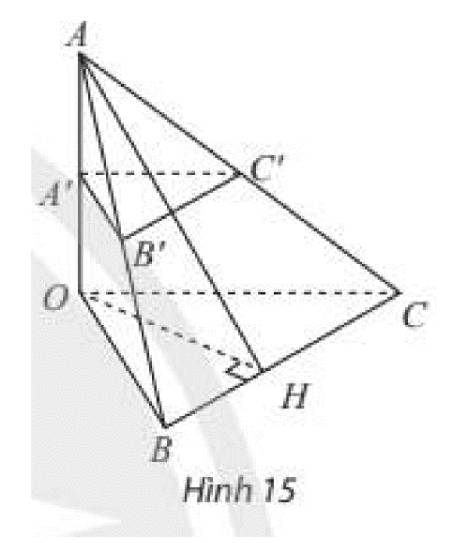
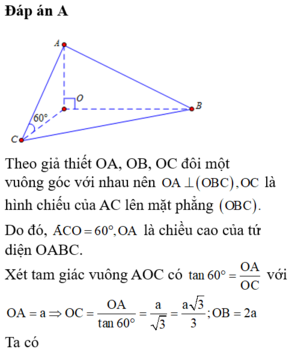
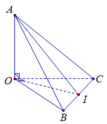
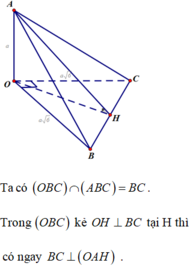
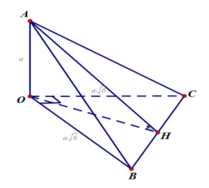
Cho tứ diện \(OABC\) có \(OA\) vuông góc với mặt phẳng \(\left( {OBC} \right)\) và có \(A',B',C'\) lần lượt là trung điểm của \(OA,AB,AC\). Vẽ \(OH\) là đường cao của tam giác \(OBC\). Chứng minh rằng:
a) \(OA \bot \left( {A'B'C'} \right)\);
b) \(B'C' \bot \left( {OAH} \right)\).

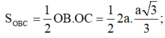
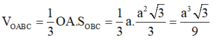
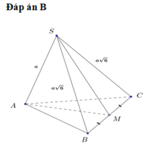


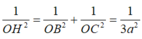

tham khảo:
a) Tam giác AOB có A'B' là đường trung bình nên A'B'//AB hay A'B'//(OBC)
Tam giác AOC có A'C' là đường trung bình nên A'C"//AC hay A'C'//(OBC)
Suy ra (A'B'C')//(OBC)
Mà OA⊥(OBC) nên OA⊥(A′B′C′)
b) Vì OA⊥(OBC);BC∈(OBC) nên OA⊥CB
Ta có đường thẳng BC vuông góc với hai đường thẳng OH và OA cắt nhau cùng thuộc (AOH) nên BC⊥(OAH)
Mà tam giác ABC có B'C' là đường trung bình nên B'C'//BC
Suy ra B′C′⊥(AOH)