Question

[hungbck5]

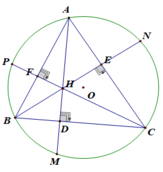
Bài 1. Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M,N,P.

1. Chứng minh rằng: Tứ giác CEHD, nội tiếp .
2. Bốn điểm B,C,E,F cùng nằm trên một đường tròn.
3. AE.AC = AH.AD; AD.BC = BE.AC.
4. H và M đối xứng nhau qua BC.
5. Xác định tâm đường tròn nội tiếp tam giác DEF.

Answer 1

[Cô Hoàng Huyền]

Cô hướng dẫn nhé.

a) Tứ giác CEHD nội tiếp vì có góc E và góc D vuông.

b) Bốn điểm B, C ,E , F cùng thuộc một đường tròn vì góc E và góc F vuông.

c) Ta có các tam giác đồng dạng : \(\Delta AEH\sim\Delta ADC\left(g-g\right)\Rightarrow\frac{AE}{AD}=\frac{AH}{AC}\Rightarrow AE.AC=AD.AH\)

Tương tự \(\Delta BEC\sim\Delta ADC\left(g-g\right)\Rightarrow\frac{BE}{AD}=\frac{BC}{AC}\Rightarrow BE.AC=AD.BC\)

d) Do \(\Delta BEC\sim\Delta ADC\Rightarrow\widehat{CBN}=\widehat{CAM}\Rightarrow\widebat{NC}=\widebat{MC}\)

Từ đó suy ra \(\widehat{HBD}=\widehat{DBM}\) hay tam giác HBM cân tại B. Vậy BD là trung trực MH hay H, M đối xứng nhau qua BC.

e) Do tứ giác BCEF nội tiếp nên \(\widehat{EFC}=\widehat{EBC}\)

Ta cũng cm được tứ giác AFDC nội tiếp nên \(\widehat{DFC}=\widehat{DAC}\)

Mà \(\widehat{EBC}=\widehat{DAC}\) nên \(\widehat{DFC}=\widehat{CFE}\) hay FH là phân giác góc F.

Tương tự có EH, DH là các đường phân giác trong tam giác DEF.

Suy ra tâm đường tròn nội tiếp tam giác DEF chính là giao điểm của EH, FH, DH và chính là điểm H.

Answer 2

[trang lê]

cô ơi  cho e hỏi câu e sao CBE = CFE vậy cô