Cho góc nhị diện có hai mặt là hai nửa mặt phẳng \(\left( P \right),\left( Q \right)\) và cạnh của góc nhị diện là đường thẳng \(d\).
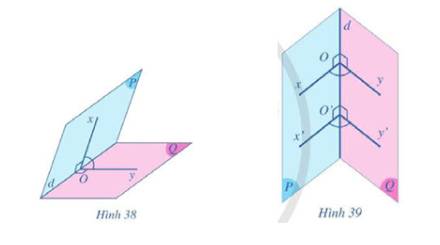
Qua một điểm \(O\) trên đường thẳng \(d\), ta kẻ hai tia \(Ox,Oy\) lần lượt thuộc hai nửa mặt phẳng \(\left( P \right),\left( Q \right)\) và cùng vuông góc với đường thẳng \(d\). Góc \(xOy\) gọi là góc phẳng nhị diện của góc nhị diện đã cho (Hình 38).
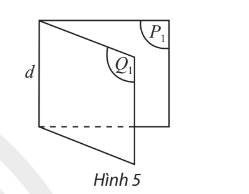
Giả sử góc \(x'Oy'\) cũng là góc phẳng nhị diện của góc nhị diện đã cho với \(O'\) khác \(O\) (Hình 39).
Hãy so sánh số đo của hai góc \(xOy\) và \(x'Oy'\).




Trong \(\left( P \right)\) ta có:
\(\left. \begin{array}{l}Ox \bot d\\O'x' \bot d\end{array} \right\} \Rightarrow Ox\parallel O'x'\)
Trong \(\left( Q \right)\) ta có:
\(\left. \begin{array}{l}Oy \bot d\\O'y' \bot d\end{array} \right\} \Rightarrow Oy\parallel O'y'\)
Vậy \(\left( {Ox,Oy} \right) = \left( {O'x',O'y'} \right)\) hay số đo của hai góc \(xOy\) và \(x'Oy'\) bằng nhau.