Đề bài
Cho \(a > 0;a \ne 1;{a^{\frac{3}{5}}} = b\)
a) Viết \({a^6};{a^3}b;\frac{{{a^9}}}{{{b^9}}}\) theo lũy thừa cơ số b
b) Tính \({\log _a}b;\,{\log _a}\left( {{a^2}{b^5}} \right);\,{\log _{\sqrt[5]{a}}}\left( {\frac{a}{b}} \right)\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ML
13 tháng 8 2023
\(4^{\log_23}=\left(2^2\right)^{\log_23}=2^{2log_23}=2^{\log_23^2}=2^{\log_29}=9\)
-> A
14 tháng 8 2023
\(P=loga^3+logb^2=log\left(a^3b^2\right)=log\left(100\right)=10\)
D
datcoder
CTVVIP
15 tháng 8 2023
a) \(\log_a\left(a^2b\right)=\log_aa^2+\log_ab=2.\log_aa+\log_ab=2.1+2=4\)
b) \(\log_a\dfrac{a\sqrt{a}}{b\sqrt[3]{a}}=\log_a\left(a\sqrt{a}\right)-\log_a\left(b\sqrt[3]{b}\right)=\log_aa^{\dfrac{3}{2}}-\log_ab^{\dfrac{4}{3}}=\dfrac{3}{2}.\log_aa-\dfrac{4}{3}\log_ab=\dfrac{3}{2}.1-\dfrac{4}{3}.2=-\dfrac{7}{6}\)
c) \(\log_a\left(2b\right)+\log_a\left(\dfrac{b^2}{2}\right)=\log_a2+\log_ab+\log_ab^2-\log_a2=\log_ab+2\log_ab=3\log_ab=3.2=6\)
14 tháng 8 2023
a: \(=log_aa^2+log_ab=2+2=4\)
b: \(log_a\left(\dfrac{a\sqrt{a}}{b\sqrt[3]{b}}\right)=log_aa^{\dfrac{3}{2}}-log_ab^{\dfrac{4}{3}}\)
=3/2-4/3*2
=3/2-8/3
=9/6-16/6=-7/6
c: \(log_a\left(2b\right)+log_a\left(\dfrac{b^2}{2}\right)\)
\(=log_a\left(2b\cdot\dfrac{b^2}{2}\right)=log_a\left(b^3\right)=3\cdot2=6\)
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 8 2023
Ta có: B là ảnh của A' lên (ABCD)
Có: D'C // A'B nên C là ảnh của D' lên (ABCD)
Từ C' kẻ C'E // CD' // A'B. Suy ra E là ảnh của C' lên (ABCD).
Vậy tam giác BCE là ảnh của tam giác A'C'D' qua phép chiếu song song lên mặt phẳng (ABCD) theo phương A'B.
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
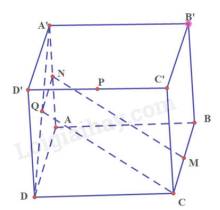
a) Ta có: N là trung điểm của AA’ nên \(\frac{{AN}}{{AA'}} = \frac{1}{2}\)
Q là trung điểm của AD’ nên \(\frac{{AQ}}{{AD'}} = \frac{1}{2}\)
Theo định lý Ta – let, ta có NQ // A’D’
Suy ra \(\frac{{NQ}}{{A'D'}} = \frac{{AN}}{{AA'}} = \frac{1}{2}\) nên\(NQ = \frac{1}{2}A'D'\)
b) Ta có: NQ // A’D’ mà A’D’ // BC nên NQ // BC hay NQ // MC (1)
Ta có \(NQ = \frac{1}{2}A'D'\) mà A’D’ = BC, \(MC = \frac{1}{2}BC\), nên NQ = MC (2)
Từ (1) và (2) suy ra MNQC là hình bình hành
c) Ta có: MNQC là hình bình hành nên MN // CQ
Mà CQ thuộc (ACD’)
Nên MN // (ACD’)
d) Gọi O là trung điểm của AC
Tam giác ACB có: O, M là trung điểm của AC, BC
Suy ra: OM // AB nên \(OM = \frac{1}{2}AB\)
Mà AB = C’D’, \(D'P = \frac{1}{2}C'D\),
Suy ra OM = D’P (1)
Ta có: OM // AB, AB // C’D’ nên OM // C’D‘ hay OM // D’P (2)
Từ (1) và (2) suy ra OMPD’ là hình bình hành. Do đó: MP // OD’
Mà OD’ thuộc (ACD’)
Suy ra: MP // (ACD’)
Mà MN thuộc (ACD’)
Do đó: (MNP) // (ACD’)
HQ
Hà Quang Minh
Giáo viên
22 tháng 8 2023
a, Hệ số góc của tiếp tuyến của đồ thị là:
\(y'\left(2\right)=-4\cdot2+1=-7\)
b, Phương trình tiếp tuyến của đồ thị (C) tại điểm M(2;-6) là:
\(y=y'\left(2\right)\cdot\left(x-2\right)-6=-7\left(x-2\right)-6=-7x+8\)
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
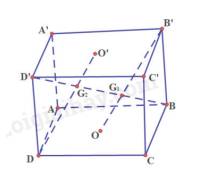
a) Ta có: AD // B’C’, AD = B’C’ nên ADC’B’ là hình bình hành
Suy ra AB’ // DC’ nên AB‘ // (A’C’D) (1)
Ta có: (ACC’A‘) là hình bình hành nên AC // A’C‘
Suy ra AC // (A’C’D‘) (2)
Mà AB‘, AC thuộc (ACB‘) (3)
Từ (1), (2), (3) suy ra (ACB‘) // (A‘C’D)
b) Gọi O, O’ lần lượt là tâm hình bình hành ABCD, A’B’C’D’
Trong (BDD’B’): B’O cắt BD’
Mà B’O thuộc (ACB’), BD’ cắt (ACB’) tại\({G_1}\)
Suy ra: B’O cắt BD’ tại\({G_1}\)
Tương tự, ta có: DO’ cắt BD’ tại\({G_2}\)
Ta có: tam giác \({G_1}OB\) đồng dạng với tam giác \({G_1}B'D'\) (do BD // B’D’)
Suy ra\(\frac{{{G_1}O}}{{{G_1}B'}} = \frac{{OB}}{{B'D'}} = \frac{1}{2}\)
Nên \(\frac{{{G_1}O}}{{{G_1}B'}} = \frac{2}{3}\)
Do đó:\({G_1}\) là trọng tâm tam giác ACB’
Chứng minh tương tự ta có:\({G_2}\) là trọng tâm tam giác A’C’D
c) Ta có tam giác\({G_1}OB\) đồng dạng với tam giác \({G_1}B'D'\)
Suy ra\(\frac{{{G_1}O}}{{{G_1}B'}} = \frac{{OB}}{{B'D'}} = \frac{1}{2}\)
Nên \({G_1}B = \frac{1}{3}BD'(1)\)
Tương tự ta có:\(\frac{{{G_2}D'}}{{{G_2}B}} = \frac{{OD'}}{{DB}} = \frac{1}{2}\)
Nên \({G_2}D' = \frac{1}{3}{\rm{DD}}'(2)\)
Từ (1) và (2) suy ra\({G_1}B = {G_1}{G_2} = {G_2}D'\)
HQ
Hà Quang Minh
Giáo viên
23 tháng 8 2023
\(A=\dfrac{x^{\dfrac{5}{4}}y+xy^{\dfrac{5}{4}}}{\sqrt[4]{x}+\sqrt[4]{y}}\\ =\dfrac{xy\left(x^{\dfrac{1}{4}}+y^{\dfrac{1}{4}}\right)}{x^{\dfrac{1}{4}}+y^{\dfrac{1}{4}}}\\ =xy\)
\(B=\left(\sqrt[7]{\dfrac{x}{y}\sqrt[5]{\dfrac{y}{x}}}\right)^{\dfrac{35}{4}}\\= \left(\sqrt[7]{\dfrac{x}{y}\cdot\left(\dfrac{x}{y}\right)^{-\dfrac{1}{5}}}\right)^{\dfrac{35}{4}}\\ =\left(\sqrt[7]{\left(\dfrac{x}{y}\right)^{\dfrac{4}{5}}}\right)^{\dfrac{35}{4}}\\ =\left[\left(\dfrac{x}{y}\right)^{\dfrac{4}{35}}\right]^{\dfrac{35}{4}}\\ =\left(\dfrac{x}{y}\right)^{\dfrac{4}{35}\cdot\dfrac{35}{4}}\\ =\left(\dfrac{x}{y}\right)^1\\ =\dfrac{x}{y}\)
a,Ta có: \(a^6=\left(a^{\dfrac{3}{5}}\right)^{10}=b^{10}\\ a^3b=\left(a^{\dfrac{3}{5}}\right)^5\cdot b=b^5\cdot b=b^6\\ \dfrac{a^9}{b^9}=\dfrac{\left(a^{\dfrac{3}{5}}\right)^{15}}{b^9}=\dfrac{b^{15}}{b^9}=b^6\)
b, \(log_ab=log_aa^{\dfrac{3}{5}}=\dfrac{3}{5}\\ log_a\left(a^2b^5\right)=log_a\left(a^2\cdot a^3\right)=log_a\left(a^5\right)=5\\ log_{\sqrt[5]{a}}\left(\dfrac{a}{b}\right)=5log_a\left(\dfrac{a}{a^{\dfrac{3}{5}}}\right)=5log_a\left(a^{\dfrac{2}{5}}\right)=2\)