Ta coi năm lấy làm mốc để tính dân số của một vùng (hoặc một quốc gia) là năm 0. Khi đó, dân số của quốc gia đó ở năm thứ t là hàm số theo biến t được cho bởi công thức \(S = A.{e^{r.t}}\). Trong đó A là dân số của vùng (hoặc quốc gia) đó ở năm O và r là tỉ lệ tăng dân số hàng năm. Biết rằng dân số Việt Nam năm 2021 ước tính là 98 564 407 người và tỉ lệ tăng dân số là 0,93%/năm. Giả sử tỉ lệ tăng dân số hàng năm là như nhau tính từ năm 2021, nêu dự đoán dân số Việt Nam năm 2030 (làm tròn kết quả đến hàng đơn vị).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dân số sẽ gấp đôi dân số của năm lấy làm mốc tính:
\(S=A.e^{r.t}\Rightarrow\dfrac{1}{r}=\ln\dfrac{S}{A}\)
Do \(S_1=2S\Rightarrow t=\dfrac{1}{r}.\ln\dfrac{2S}{S}=\dfrac{1}{r}.\ln2\)

Dân số của nước này sau 20 năm là;
\(A=19\cdot2^{\dfrac{20}{30}}\simeq30\)(triệu người)

Đáp án D
Thay các số liệu vào phương trình mũ đã cho ta được
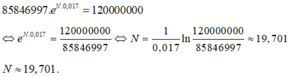
Đề bài tính từ 1/1/2009 do đó cộng thêm 19,701 năm ta được đến năm 2028, dân số của nước ta ở mức 120 triệu người.

Đáp án C
Thay các số liệu vào phương trình mũ đã cho ta được
 do đó cộng thêm 19,701 năm ta được đến năm 2028, dân số của nước ta ở mức 120 triệu người.
do đó cộng thêm 19,701 năm ta được đến năm 2028, dân số của nước ta ở mức 120 triệu người.

Đáp án D
S 0 = S 2010
Theo giả thiết
S 2015 = S 2010 . e 5 r S 2015 = S 2010 . e 15 r ⇒ e 5 r = S 2015 S 2010
S 2015 = S 2010 . S 2015 S 2010 3 ≈ 1424227

Giả sử dân số của quốc gia đó từ năm 2011 đến năm 2021 là dãy số \(\left( {{u_n}} \right)\) với \({u_1} = P\).
Ta có:
\(\begin{array}{l}{u_1} = P\\{u_2} = {u_1} + {u_1}.\frac{a}{{100}} = {u_1}.\left( {1 + \frac{a}{{100}}} \right)\\{u_3} = {u_2} + {u_2}.\frac{a}{{100}} = {u_2}\left( {1 + \frac{a}{{100}}} \right)\\{u_4} = {u_3} + {u_3}.\frac{a}{{100}} = {u_3}\left( {1 + \frac{a}{{100}}} \right)\\ \vdots \\{u_{11}} = {u_{10}} + {u_{10}}.\frac{a}{{100}} = {u_{10}}\left( {1 + \frac{a}{{100}}} \right)\end{array}\)
Vậy dân số các năm từ năm 2011 đến năm 2021 của quốc gia đó tạo thành cấp số nhân với công bội \(q = 1 + \frac{a}{{100}}\).



Dân số Việt Nam năm 2030 vào khoảng:
\(S=98564407\cdot e^{0,93\%\cdot9}=107169341\left(người\right)\)