Cho hình thang cân ABCD( AB//CD,AB < CD ). Kẻ đường cao AH,BK của hình thang. Chứng minh rằng:
a. Chứng minh ΔAHD = ΔBKC . ( Hình 4)
b) Chứng minh AB = HK
c) Chỉ ra: KC= (AB - BD):2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác ADH và tam giác BCK có:
góc AHD= góc BKC
DA= BC (ABCD là hình thang cân)
góc D = góc C (ABCD là htc)
=> tam giác ADH = tam giác BCK (ch-gn)
=> HD = KC (đpcm)


Áp dụng định nghĩa, tính chất và giả thiết của hình thang cân ta có:
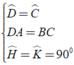
⇒ Δ ADH = Δ BCK
(trường hợp cạnh huyền – góc nhọn)
⇒ DH = CK (cặp cạnh tương ứng bằng nhau)
Vậy DH = CK. (đpcm)


Câu 1:
Xét ΔAED vuông tại E và ΔBFC vuông tại F có
AD=BC
góc D=góc C
Do đó: ΔAED=ΔBFC
Suy ra: DE=CF
Bài 2:
b: Xét ΔBAD và ΔABC có
AB chung
AD=BC
BD=AC
Do đó: ΔBAD=ΔABC
Suy ra: góc EAB=góc EBA
=>ΔEAB cân tại E
=>EA=EB
a: Xét ΔAHD vuông tại H và ΔBKC vuông tại K có
AD=BC
góc D=góc C
=>ΔAHD=ΔBKC
b: Xét tứ giác ABKH có
AB//KH
AH//BK
=>ABKH là hình bình hành
=>AB=KH
còn câu c thì sao ạ?