Cho tam giác ABC vuông tại A. Đường cao AH. Lấy I là trung điểm của AC.
a) Chứng minh I là giao điểm của 3 đường trung trực tam giác AHC. Gọi K và D lần lượt là trung điểm của AH và HC. Chứng minh KD // AC.
b) Chứng minh BK vuông góc với AD.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ta có: ΔAHC vuông tại H
mà HI là trung tuyến nên HI=CI=AI
=>I là giao điểm của ba đường trung trực
b: Xét ΔHAC có
D là trung điểm của HC
K là trung điểm của AH
Do đó: DK là đường trung bình
=>DK//AC
c: Có:
DK//AC
AC vuông góc AB
=>DK vuông góc AB
Xét ΔBAD có
DK,AH là đường cao
DK cắt AH tại K
=>K là trực tâm
=>BK vuông góc AD

a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
Do đó: ADHE là hình chữ nhật
Suy ra: AH=DE

b: Xét tứ giác AIHK có
\(\widehat{KAI}=\widehat{AIH}=\widehat{AKH}=90^0\)
Do đó: AIHK là hình chữ nhật
Suy ra: IK=AH

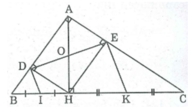
Tam giác BDH vuông tại D có DI là đường trung tuyến thuộc cạnh huyền BH
⇒ DI = IB = 1/2 BH (tính chất tam giác vuông)
⇒ ∆ IDB cân tại I ⇒ ∠ (DIB) = 180 0 - 2. ∠ B (1)
Tam giác HEC vuông tại E có EK là đường trung tuyến thuộc cạnh huyền HC.
⇒ EK = KH = 1/2 HC (tính chất tam giác vuông) .
⇒ ∆ KHE cân tại K ⇒ ∠ (EKH) = 180 0 - 2. ∠ (KHE) (2)
Tứ giác ADHE là hình chữ nhật nên:
HE // AD hay HE // AB ⇒ ∠ B = ∠ (KHE) (đồng vị)
Từ (1), (2) và (3) suy ra: ∠ (DIB) = ∠ (EKH)
Vậy DI // EK (vì có cặp góc đồng vị bằng nhau).

a: Xét ΔABC có
E là trung điểm của AB
K là trung điểm của AC
Do đó: KE là đường trung bình của ΔABC
c: Ta có: KE là đường trung bình của ΔBAC
nên \(KE=\dfrac{BC}{2}=\dfrac{10}{2}=5\left(cm\right)\)
a: ΔHAC vuông tại H
=>ΔHAC nội tiếp đường tròn đường kính AC
=>I là giao điểm của 3 đường trung trực của ΔAHC
Xét ΔHAC có HK/HA=HD/HC
nên KD//AC
b: DK//AC
AC vuông góc AB
=>DK vuông góc AB
Xét ΔBAD có
DK,AH là đường cao
DK cắt AH tại K
=>K là trực tâm
=>BK vuông góc AD