Cho tam giác ABC vuông tại A (AB > AC), đường cao AH
b) Biết \(\widehat{C}\) \(=60^0\), AC = 8, AB = 12. Giải tam giác HAB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 8 2023
a: ΔABC vuông tại A có AH là đường cao
nên AB^2=BH*BC; AC^2=CH*CB
=>AB^2/AC^2=BH/CH
b:
góc B=90-60=30 độ
góc HAB=90-30=60 độ
BC=căn 8^2+12^2=4*căn 13(cm)
HB=AB^2/BC=36/căn 13(cm)
AH=8*12/4*căn 13=24/căn 13(cm)
19 tháng 4 2023
a: \(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
AH=12*16/20=192/20=9,6cm
b: Xét ΔBHA vuông tại H và ΔBAC vuông tại A có
góc B chung
=>ΔBHA đồng dạng với ΔBAC
11 tháng 2 2022
a:
BC=35cm
\(AH=\dfrac{AB\cdot AC}{BC}=16.8\left(cm\right)\)
b: \(AE=\dfrac{AH^2}{AC}=\dfrac{16.8^2}{28}=10.08\left(cm\right)\)
\(AD=\dfrac{AH^2}{AB}=\dfrac{16.8^2}{21}=13.44\left(cm\right)\)
Do đó: \(S_{AED}=\dfrac{AD\cdot AE}{2}=\dfrac{13.44\cdot10.08}{2}=67.7376\left(cm^2\right)\)
17 tháng 9 2023
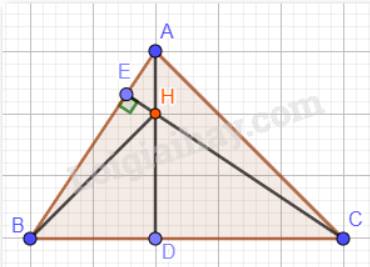
Ta có: AB < AC nên \(\widehat {ACB} < \widehat {ABC}\) (góc ACB đối diện với cạnh AB; góc ABC đối diện với cạnh AC)
Mà tam giác ADB và tam giác ADC vuông tại D.
Vì tổng hai góc nhọn trong một tam giác vuông bằng 90°.
Mà \(\widehat {ACB} < \widehat {ABC}\).
Suy ra: \(90^\circ - \widehat {ACB} > 90^0 - \widehat {ABC}\) hay \(\widehat {DAC} > \widehat {DAB}\).
Vậy \(\widehat {HAC} > \widehat {HAB}\) hay \(\widehat {HAB} < \widehat {HAC}\).
Suy ra: A, B, D sai.
Đáp án: C.\(\widehat {HAB} = \widehat {HCB}\).
19 tháng 7 2021
a) Xét ΔABC vuông tại B và ΔAHB vuông tại H có
\(\widehat{A}\) chung
Do đó: ΔABC\(\sim\)ΔAHB(g-g)
Suy ra: \(\dfrac{AB}{AH}=\dfrac{AC}{AB}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AB^2=AH\cdot AC\)
b) Ta có: \(AB^2=AH\cdot AC\)
\(\Leftrightarrow AH\cdot12=6^2=36\)
hay AH=3(cm)
24 tháng 3 2023
Xét \(\Delta ABC\&\Delta ABH\) ta có:
\(\widehat{A}=\widehat{B}=90^o\left(gt\right)\\ \widehat{B}=\widehat{B}\\\Rightarrow \Delta ABC\&\sim ABH\)
KV
24 tháng 3 2023
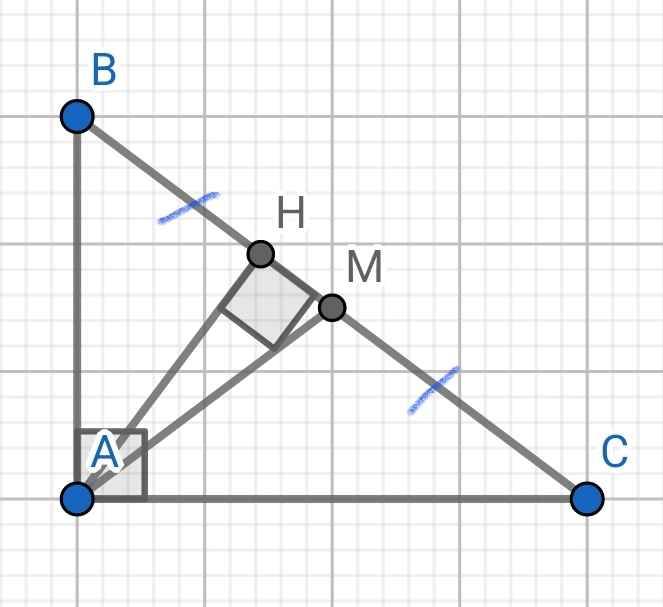
Xét ∆AHB và ∆CBA có:
∠AHB = ∠CAB = 90⁰
∠B chung
⇒ ∆AHB ∽ ∆CBA (g-g)
28 tháng 4 2023
a: Xet ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
HB=6^2/10=3,6cm
góc B=90-60=30 độ
góc HAB=90-30=60 độ
BC=căn 8^2+12^2=4*căn 13(cm)
HB=AB^2/BC=36/căn 13(cm)
AH=8*12/4*căn 13=24/căn 13(cm)