cho tam giác ABC có AB =3cm AC=4cm BC=5cm. Tính các góc trong tam giác ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 12 2021
bài 2:
ta có: AB<AC<BC(Vì 3cm<4cm<5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
LN
Lưu Nguyễn Hà An
CTVHS
15 tháng 2 2022
bài 2:
ta có: AB <AC <BC (Vì 3cm <4cm <5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
HT mik làm giống bạn Dương Mạnh Quyết
PT
1
CM
21 tháng 9 2018
Ta có: AB = 3 ⇒ A B 2 = 3 2 = 9
AC = 4 ⇒ A C 2 = 4 2 = 16
BC = 5 ⇒ B C 2 = 5 2 = 25
Ta có: A B 2 + A C 2 = 9 + 16 = 25 = B C 2
Suy ra tam giác ABC vuông tại A.
Ta có:
TT
0
28 tháng 7 2021
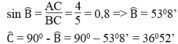
a) Xét ΔABC có
\(BC^2=AB^2+AC^2\left(5^2=3^2+4^2\right)\)
nên ΔABC vuông tại A(Định lí Pytago đảo)
Xét ΔABC vuông tại A có
\(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{4}{5}\)
nên \(\widehat{C}\simeq53^0\)
\(\Leftrightarrow\widehat{B}=37^0\)
b) Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
hay \(\dfrac{BD}{4}=\dfrac{CD}{3}\)
mà BD+CD=5
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{4}=\dfrac{CD}{3}=\dfrac{BD+CD}{4+3}=\dfrac{5}{7}\)
Do đó: \(BD=\dfrac{20}{7}cm;CD=\dfrac{15}{7}cm\)
NL
0
17 tháng 8 2023
3:
góc C=90-50=40 độ
Xét ΔABC vuông tại A có sin C=AB/BC
=>4/BC=sin40
=>\(BC\simeq6,22\left(cm\right)\)
\(AC=\sqrt{BC^2-AB^2}\simeq4,76\left(cm\right)\)
1:
góc C=90-60=30 độ
Xét ΔABC vuông tại A có
sin B=AC/BC
=>3/BC=sin60
=>\(BC=\dfrac{3}{sin60}=2\sqrt{3}\left(cm\right)\)
=>\(AB=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\left(cm\right)\)
CM
15 tháng 1 2019
Suy ra: tam giác ABC vuông tại A.
Diện tích tam giác ABC là:
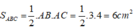
*Gọi tam giác ABC đồng dạng với tam giác MNP theo tỉ số k
Suy ra:
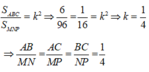
Thay số
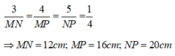
Chọn đáp án B
Xét tam giác ABC : \(AB^2+AC^2=3^2+4^2=5^2=BC^2\)
\(\Rightarrow\Delta ABC\) vuông tại A \(\Rightarrow\widehat{A}=90^o\)
\(sinB=\dfrac{AC}{BC}=\dfrac{4}{5}\\ \Rightarrow\widehat{B}=53^o8'\)
\(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\\ \Rightarrow\widehat{C}=36^o52'\)
Theo định lí pytago ta có: \(AB^2+AC^2=BC^2=9+16=BC^2=25\)
⇒ Tam giác ABC vuông tại A ⇒ \(\widehat{A}=90^\circ\)
Theo tỉ lệ thức trong tam giác vuông:
\(sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{4}{5}=0,8\approx53^{\circ}\)
\(\widehat{C}=90^{\circ}-53^{\circ}=37^{\circ}\)