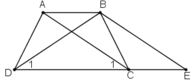
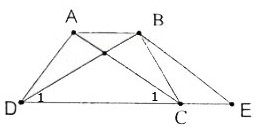
Chứng minh định lí "Hình thang có hai đường chéo bằng nhau là hình thang cân" qua bài toán sau: Cho hình thang ABCD (AB = CD) có AC = BD.Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại E. Chứng mình rằng:a) ∆BDE là tam giác cân.b) ∆ACD = ∆BDC.c) Hình thang ABCD là hình thang cân.CÁC BẠN GIẢI BÀI NÀY CÂU a) BẰNG CÁCH XÉT HAI TAM GIÁC GIÚP MK VS NHÉ ! CHỈ CẦN CÂU a) THÔI !!!! GIẢI BẰNG CÁCH XÉT...
Đọc tiếp
Chứng minh định lí "Hình thang có hai đường chéo bằng nhau là hình thang cân" qua bài toán sau: Cho hình thang ABCD (AB = CD) có AC = BD.
Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại E. Chứng mình rằng:
a) ∆BDE là tam giác cân.
b) ∆ACD = ∆BDC.
c) Hình thang ABCD là hình thang cân.
CÁC BẠN GIẢI BÀI NÀY CÂU a) BẰNG CÁCH XÉT HAI TAM GIÁC GIÚP MK VS NHÉ ! CHỈ CẦN CÂU a) THÔI !!!! GIẢI BẰNG CÁCH XÉT HAI TAM GIÁC SAU ĐÓ SUY RA HAI CẠNH BẰNG NHAU ! GIÚP MK VS!
= 
(3)
= 
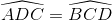
a, Ta có: BE song song AC ( theo bài ra)
AB song song CE ( E thuộc CD)
nên ABEC là hình bình hành, do đó AC=BE
mà AC = BD
nên BD=BE do đó BDE là tam giác cân
b, Ta có AC song song BE nên ˆBEC=ˆACD
mà ˆBED=ˆBDC ( BDE là tam giác cân )
do đó ˆACD=ˆBDC
Xét tg ACD và tg BDC có : ˆACD=ˆBDC
AC=BD( theo gt )
BC là cạnh chung
nên tg ACD =tg BDC ( c-g-c)
c, Theo chứng minh câu b, ta có: tg ACD= tg BDC
do đó ˆADC=ˆBCD
Vậy ABCD là hình thang cân
lạc yêu cầu r bn cóp mạng ghê đấy