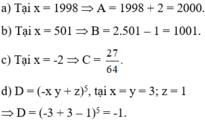( x-1)3 - 4x ( x+1) (x-1) ( x2 + x + 1 ) tại x = -2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 7 2021
1) \(\left(\dfrac{1}{2}x+3\right)\left(x^2-4x-6\right)\)
\(=\dfrac{1}{2}x^3-2x^2-3x+3x^2-12x-18\)
\(=\dfrac{1}{2}x^3+x^2-15x-18\)
2) \(\left(6x^2-9x+15\right)\left(\dfrac{2}{3}x+1\right)\)
\(=4x^3+6x^2-6x^2-9x+10x+15\)
\(=4x^3+x+15\)
3) Ta có: \(\left(3x^2-x+5\right)\left(x^3+5x-1\right)\)
\(=3x^5+15x^2-3x^2-x^4-5x^2+x+5x^3+25x-5\)
\(=3x^5-x^4+5x^3+10x^2+26x-5\)
4) Ta có: \(\left(x-1\right)\left(x+1\right)\left(x-2\right)\)
\(=\left(x^2-1\right)\left(x-2\right)\)
\(=x^3-2x^2-x+2\)
18 tháng 10 2021
\(A=x^2+4x-21-x^2-4x+5=-16\\ B=-2\left(4x^2+20x+25\right)-\left(1-16x^2\right)\\ B=-8x^2-40x-50-1+16x^2=8x^2-40x-51\\ C=x^2\left(x^2-16\right)-\left(x^4-1\right)=x^4-16x^2-x^4+1=1-16x^2\\ D=x^3+1-\left(x^3-1\right)=2\\ E=x^3-3x^2+3x-1-x^3+1-9x^2+1=-12x^2+3x+1\)
NH
1
5 tháng 3 2022
\(\left(2x+1\right)^2=x^2\Leftrightarrow\left[{}\begin{matrix}2x+1=x\\2x+1=-x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-\dfrac{1}{3}\end{matrix}\right.\)
\(3x-4x^2+6-8x=x^2+4x+6\Leftrightarrow5x^2+9x=0\Leftrightarrow x=0;x=-\dfrac{9}{5}\)
đk : x khác 0 ; -1
\(\Rightarrow x^2+3x+x^2-x-2=2x\left(x+1\right)\Leftrightarrow2x-2=2x\left(voli\right)\)
Vậy pt vô nghiệm
TA
2 tháng 3 2021
1) `x^2+4-2(x-1)=(x-2)^2`
`<=>x^2+4-2x+2=x^2-4x+4`
`<=>-2x+2=-4x`
`<=>2x=-2`
`<=>x=-1`
.
2) ĐKXĐ: `x \ne \pm 3`
`(x+3)/(x-3)-(x-1)/(x+3)=(x^2+4x+6)/(x^2-9)`
`<=>(x+3)^2-(x-1)(x-3)=x^2+4x+6`
`<=>x^2+6x+9-x^2+4x-3=x^2+4x+6`
`<=>10x+6=x^2+4x+6`
`<=>x^2-6x=0`
`<=>x(x-6)=0`
`<=>x=0;x=6`
.
3) ĐKXĐ: `x \ne \pm 3`
`(3x-3)/(x^2-9) -1/(x-3 )= (x+1)/(x+3)`
`<=>(3x-3)-(x+3)=(x+1)(x-3)`
`<=> 2x-6=x^2-2x-3`
`<=>x^2-4x+3=0`
`<=>x^2-x-3x+3=0`
`<=>x(x-1)-3(x-1)=0`
`<=>(x-3)(x-1)=0`
`<=> x=3;x=1`
Vậy...
30 tháng 7 2021
1)(x2-4x+16)(x+4)-x(x+1)(x+2)+3x2=0
\(\Rightarrow\)(x3+64)-x(x2+2x+x+2)+3x2=0
\(\Rightarrow\)x3+64-x3-2x2-x2-2x+3x2=0
\(\Rightarrow\)-2x+64=0
\(\Rightarrow\)-2x=-64
\(\Rightarrow\)x=\(\dfrac{-64}{-2}\)
\(\Rightarrow x=32\)
30 tháng 7 2021
2)(8x+2)(1-3x)+(6x-1)(4x-10)=-50
\(\Rightarrow\)8x-24x2+2-6x+24x2-60x-4x+10=50
\(\Rightarrow\)-62x+12=50
\(\Rightarrow\)-62x=50-12
\(\Rightarrow\)-62x=38
\(\Rightarrow\)x=\(-\dfrac{38}{62}=-\dfrac{19}{31}\)
KV
17 tháng 12 2023
a) x³y + x - y - 1
= (x³y - y) + (x - 1)
= y(x³ - 1) + (x - 1)
= y(x - 1)(x² + x + 1) + (x - 1)
= (x - 1)[y(x² + x + 1) + 1]
= (x - 1)(x²y + xy + y + 1)
b) x²(x - 2) + 4(2 - x)
= x²(x - 2) - 4(x - 2)
= (x - 2)(x² - 4)
= (x - 2)(x - 2)(x + 2)
= (x - 2)²(x + 2)
c) x³ - x² - 20x
= x(x² - x - 20)
= x(x² + 4x - 5x - 20)
= x[(x² + 4x) - (5x + 20)]
= x[x(x + 4) - 5(x + 4)]
= x(x + 4)(x - 5)
d) (x² + 1)² - (x + 1)²
= (x² + 1 - x - 1)(x² + 1 + x + 1)
= (x² - x)(x² + x + 2)
= x(x - 1)(x² + x + 2)
KV
17 tháng 12 2023
e) 6x² - 7x + 2
= 6x² - 3x - 4x + 2
= (6x² - 3x) - (4x - 2)
= 3x(2x - 1) - 2(2x - 1)
= (2x - 1)(3x - 2)
f) x⁴ + 8x² + 12
= x⁴ + 2x² + 6x² + 12
= (x⁴ + 2x²) + (6x² + 12)
= x²(x² + 2) + 6(x² + 2)
= (x² + 2)(x² + 6)
g) (x³ + x + 1)(x³ + x) - 2
Đặt u = x³ + x
x³ + x + 1 = u + 1
(u + 1).u - 2
= u² + u - 2
= u² - u + 2u - 2
= (u² - u) + (2u - 2)
= u(u - 1) + 2(u - 1)
= (u - 1)(u + 2)
= (x³ + x - 1)(x³ + x + 2)
= (x³ + x - 1)(x³ + x² - x² - x + 2x + 2)
= (x³ + x - 1)[(x³ + x²) - (x² + x) + (2x + 2)]
= (x³ + x - 1)[x²(x + 1) - x(x + 1) + 2(x + 1)]
= (x³ + x - 1)(x - 1)(x² - x + 2)
h) (x + 1)(x + 2)(x + 3)(x + 4) - 1
= [(x + 1)(x + 4)][(x + 2)(x + 3)] - 1
= (x² + 5x + 4)(x² + 5x + 6) - 1 (1)
Đặt u = x² + 5x + 4
u + 2 = x² + 5x + 6
(1) u.(u + 2) - 1
= u² + 2u - 1
= u² + 2u + 1 - 2
= (u² + 2u + 1) - 2
= (u + 1)² - 2
= (u + 1 + √2)(u + 1 - √2)
= (x² + 5x + 4 + 1 + √2)(x² + 5x + 4 + 1 - √2)
= (x² + 5x + 5 + √2)(x² + 5x + 5 - √2)
TK
1
NG
2 tháng 11 2016
Vì x=3
A=(x-1)2x-4x(x-1)+4x(x-1)
A=(x-1)2x
A=2x2-2x
A=2x(x-1)
A=2.3(3-1)
A=12
tớ thu gọn luôn -4x với +4x nên =0 cậu ak
