a) Sử dụng biểu đồ ở Hoạt động mở đầu, hoàn thiện bảng thống kê sau:
b) Tìm các nhóm chứa giá trị trung vị chiều cao thành viên mỗi đội.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 7 2023
| Khoảng tuổi | [20;30) | [30;40) | [40;50) | [50;60) | [60;70) |
| Số khách | 3 | 9 | 6 | 4 | 2 |
19 tháng 10 2023
Tham khảo:
a)
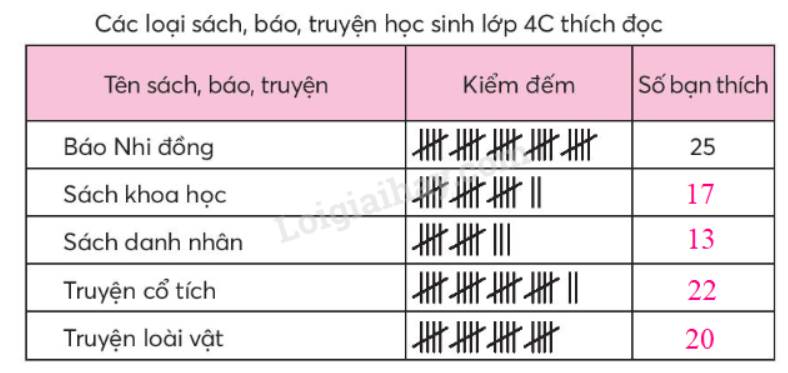
b) Hoàn thiện biểu đồ:
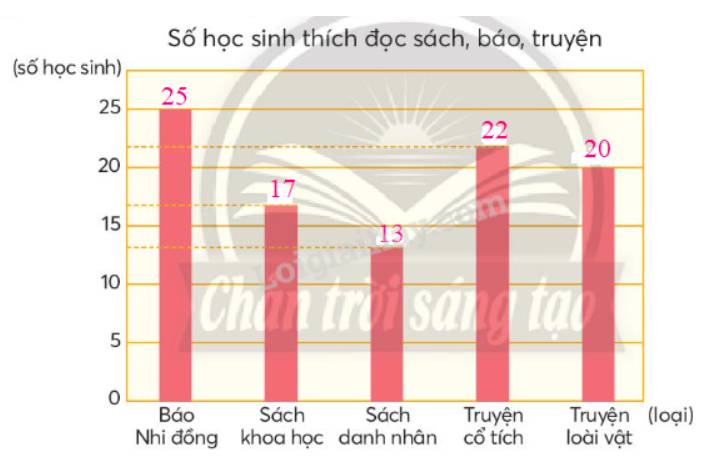
Trong các loại sách, báo, truyện được tìm hiểu, học sinh lớp 4C thích đọc báo nhi đồng nhất.
KV
19 tháng 10 2023
a)
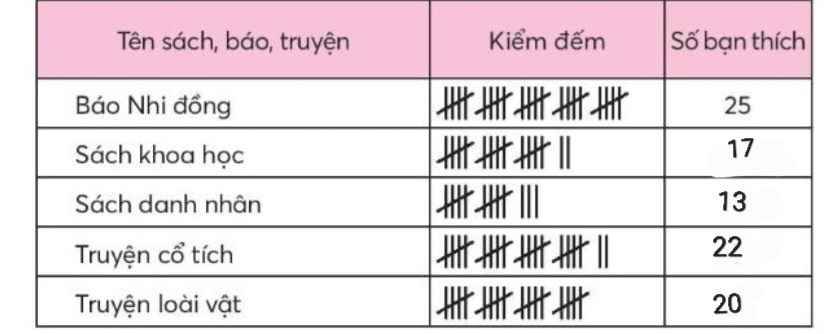b)
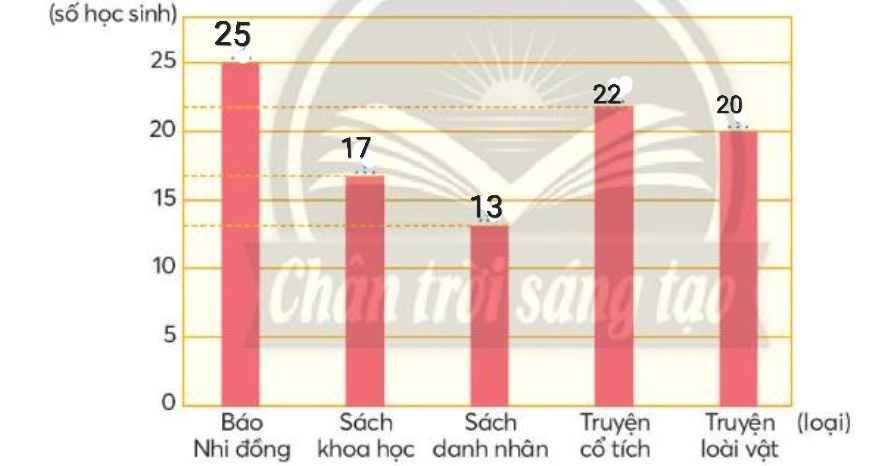Trong các loại sách, báo, truyện được tìm hiểu, học sinh lớp 4C thích đọc Báo Nhi Đồng nhất
QT
Quoc Tran Anh Le
Giáo viên
11 tháng 1
Chi tiêu hợp lí thì nên đặt chi tiêu vào những khoản ưu tiên, cần thiết và có một khoản tiết kiệm:
• Các khoản chi tiêu cho học tập của các con, dịch vụ y tế và chăm sóc sức khỏe chiếm khoảng 30%;
• Các nhu cầu thiết yếu nên chiếm khoảng 30%;
• Chi tiêu cho mua sắm cá nhân nên chiếm khoảng 20%;
• Khoản tiết kiệm nên chiếm khoảng 20%.
Từ đó mỗi thành viên trong nhóm và những ý kiến thống nhất sau khi thảo luận.
Sau đó, tiến hành lập bảng thống kê các khoản chi tiêu của gia đình trên trong vòng một tuần theo mẫu như ở Bảng 3.
19 tháng 10 2023
Tham khảo:
a) Biểu đồ cột ở bên biểu diễn số học sinh các khối lớp của trường em.
b)
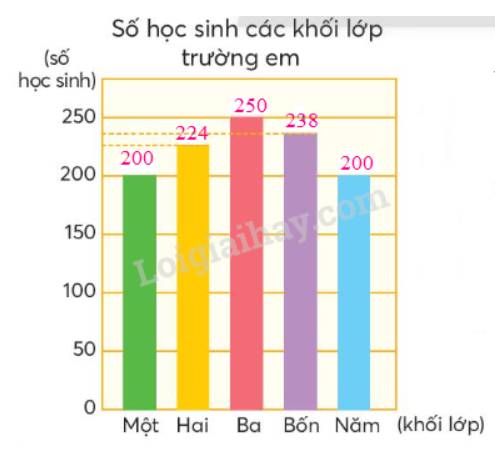
c) Số học sinh khối lớp Hai nhiều hơn số học sinh khối lớp Một.
Số học sinh khối lớp Năm ít hơn số học sinh khối lớp Ba.
....
d) Tên các khối lớp theo thứ tự số học sinh từ ít đến nhiều là: Khối Một (Khối Năm), Khối Hai, Khối Bốn, Khối Ba.
22 tháng 9 2023
Tham khảo:
a) Sắp xếp lại dãy số liệu theo thứ tự không giảm:
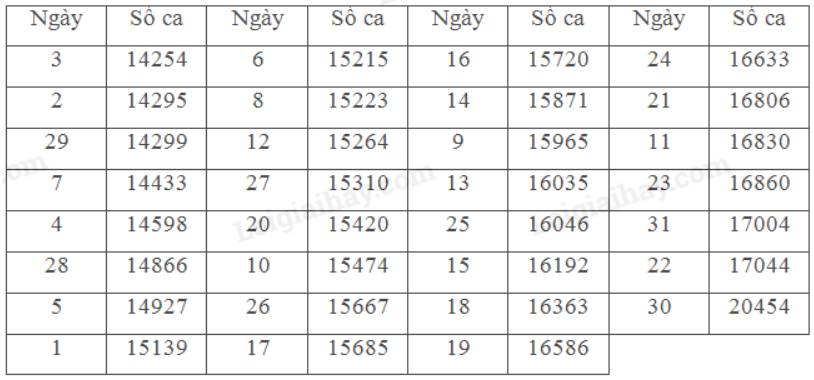
Số trung bình của số liệu là: \(\bar x \approx 15821,87\)
Tứ phân vị thứ nhất là: \({x_8} = 15139\)
Tứ phân vị thứ hai là: \({x_{16}} = 15685\)
Tứ phân vị thứ ba là: \({x_{24}} = 16586\)
Mẫu số liệu có 1 giá trị ngoại lệ.
b)
c) Ta có:
• Số ca nhiễm mới SARS-CoV-2 trung bình trong tháng 12/2021 tại Việt Nam là:
\(\bar x = \frac{{14.14,74 + 14.16,25 + 2.17,75 + 0.19,25 + 1.20,75}}{{31}} \approx 15,81\)
• Gọi \({x_1};{x_2};...;{x_{31}}\) số ca nhiễm mới SARS-CoV-2 mỗi ngày trong tháng 12/2021 tại Việt Nam được xếp theo thứ tự không giảm.
Ta có: \({x_1},...,{x_{14}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}{\begin{array}{*{20}{c}}{\left[ {14;15,5} \right)}\end{array}}\end{array}}\end{array};{x_{15}},...,{x_{28}} \in \begin{array}{*{20}{l}}{\begin{array}{*{20}{c}}{\left[ {15,5;17} \right)}\end{array}}\end{array};{x_{29}},{x_{30}} \in \begin{array}{*{20}{c}}{\left[ {17;18,5} \right)}\end{array};{x_{31}} \in \begin{array}{*{20}{l}}{\begin{array}{*{20}{c}}{\left[ {20;21,5} \right)}\end{array}}\end{array}\)
Tứ phân vị thứ hai của dãy số liệu là: \({x_{16}}\)
Ta có: \(n = 31;{n_m} = 14;C = 14;{u_m} = 15,5;{u_{m + 1}} = 17\)
Do \({x_{16}} \in \begin{array}{*{20}{c}}{\left[ {15,5;17} \right)}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 15,5 + \frac{{\frac{{31}}{2} - 14}}{{14}}.\left( {17 - 15,5} \right) \approx 15,66\)
Tứ phân vị thứ nhất của dãy số liệu là: \({x_8}\).
Ta có: \(n = 31;{n_m} = 14;C = 0;{u_m} = 14;{u_{m + 1}} = 15,5\)
Do \({x_8} \in \begin{array}{*{20}{c}}{\left[ {14;15,5} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 14 + \frac{{\frac{{31}}{4} - 0}}{{14}}.\left( {15,5 - 14} \right) \approx 14,83\)
Tứ phân vị thứ ba của dãy số liệu là: \({x_{24}}\).
Ta có: \(n = 31;{n_j} = 14;C = 14;{u_j} = 15,5;{u_{j + 1}} = 17\)
Do \({x_{24}} \in \begin{array}{*{20}{c}}{\left[ {15,5;17} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 15,5 + \frac{{\frac{{3.31}}{4} - 14}}{{14}}.\left( {17 - 15,5} \right) \approx 16,49\)
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
a) \(y = {\left( {\frac{1}{2}} \right)^x}\)
a) Biểu diễn các điểm ở câu a:
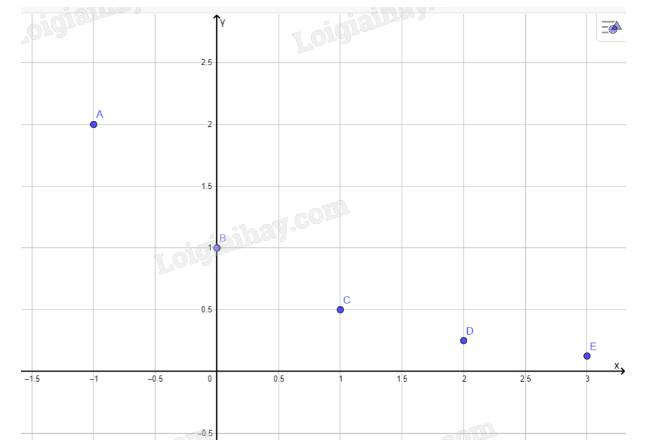
b) Tọa độ giao điểm của đồ thị hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\) với trục tung là (0;1)
Đồ thị hàm số đó không cắt trục hoành
c) \(\mathop {\lim }\limits_{x \to + \infty } {\left( {\frac{1}{2}} \right)^x} = 0;\,\,\mathop {\lim }\limits_{x \to - \infty } {\left( {\frac{1}{2}} \right)^x} = + \infty \)
Hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\) nghịch biến trên toàn \(\mathbb{R}\)
Bảng biến thiên của hàm số:
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
a) Bảng số liệu thống kê lượng mưa trung bình tháng ở Cần Thơ:
Tháng | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Lượng mưa (mm) | 6,1 | 1,9 | 13,3 | 36,5 | 167,7 | 222,6 | 239,2 | 231,0 | 252,1 | 275,3 | 150,1 | 39,7 |
b)Tổng lượng mưa trung bình năm ở Cần Thơ là:
\(6,1 + 1,9 + 13,3 + 36,5 + 167,7 + 222,6 + 239,2 + 231,0 + 252,1 + 275,3 + 150,1 + 39,7 = 1635,5\)(mm)
c) Ba tháng có lượng mưa trung bình tháng lớn nhất ở Cần Thơ là: tháng 10 (275,3 mm); tháng 9 (252,1 mm) và tháng 7 (239,2 mm).
d) Ba tháng khô hạn nhất ở Cần Thơ là: tháng 2 (1,9 mm); tháng 1 (6,1 mm) và tháng 3 (13,3 mm).
a)
b) Nhóm chứa giá trị trung vị chiều cao thành viên đội Sao La là \(\begin{array}{*{20}{l}}{\;\left[ {180;185} \right)}\end{array}\).
Nhóm chứa giá trị trung vị chiều cao thành viên đội Kim Ngưu là \(\begin{array}{*{20}{l}}{\;\left[ {185;190} \right)}\end{array}\).