Đọc, quan sát, thảo luận để biết một số quy tắc đơn giản tính độ phức tạp thời gian thuật toán.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
Quoc Tran Anh Le
Giáo viên
23 tháng 8 2023
Đánh giá được mức đơn giản của thuật toán, từ đó tìm ra được cách giải nhanh nhất.
QT
Quoc Tran Anh Le
Giáo viên
23 tháng 8 2023
Thuật toán tìm kiếm nhị phân thực hiện tìm kiếm một mảng đã sắp xếp bằng cách liên tục chia các khoảng tìm kiếm thành 1 nửa. Bắt đầu với một khoảng từ phần tử đầu mảng, tới cuối mảng. Nếu giá trị của phần tử cần tìm nhỏ hơn giá trị của phần từ nằm ở giữa khoảng thì thu hẹp phạm vi tìm kiếm từ đầu mảng tới giửa mảng và nguợc lại. Cứ thế tiếp tục chia phạm vi thành các nửa cho dến khi tìm thấy hoặc đã duyệt hết.
Thuật toán tìm kiếm nhị phân tỏ ra tối ưu hơn so với tìm kiếm tuyết tính ở các mảng có độ dài lớn và đã được sắp xếp. Ngược lại, tìm kiếm tuyến tính sẽ tỏ ra hiệu quả hơn khi triển khai trên các mảng nhỏ và chưa được sắp xếp.
QT
Quoc Tran Anh Le
Giáo viên
23 tháng 8 2023
Tính đúng của thuật toán cần được chứng minh bằng lập luận toán học. Sử dụng các bộ dữ liệu kiểm thử có thể làm tăng độ tin cậy của chương trình nhưng chưa chứng minh được tính đúng của thuật toán.
QT
Quoc Tran Anh Le
Giáo viên
23 tháng 8 2023
Thuật toán là một chuỗi các bước được thiết kế để giải quyết một vấn đề cụ thể. Một trong những yếu tố quan trọng để đánh giá hiệu suất của một thuật toán là độ phức tạp thời gian, tức là thời gian mà thuật toán mất để thực thi dựa trên kích thước đầu vào của vấn đề. Phân loại thuật toán dựa trên độ phức tạp thời gian là một phương pháp được sử dụng phổ biến để đánh giá và so sánh hiệu suất của các thuật toán khác nhau. Dưới đây là một số phân loại chính dựa trên độ phức tạp thời gian của thuật toán:
-O(1) (độ phức tạp thời gian hằng số): Đây là loại thuật toán có thời gian thực thi không thay đổi theo kích thước đầu vào. Thời gian thực thi của thuật toán này là cố định, vì vậy độ phức tạp thời gian là hằng số. Ví dụ: Truy cập vào phần tử trong mảng có kích thước cố định.
-O(log n) (độ phức tạp thời gian logarithmic): Đây là loại thuật toán có thời gian thực thi tăng theo logarit của kích thước đầu vào. Thuật toán này thường được sử dụng trong các bài toán tìm kiếm nhị phân, các thuật toán chia để trị, hoặc các thuật toán sắp xếp hiệu quả như QuickSort hoặc MergeSort.
-O(n) (độ phức tạp thời gian tuyến tính): Đây là loại thuật toán có thời gian thực thi tăng tỷ lệ trực tiếp với kích thước đầu vào. Ví dụ: Duyệt qua từng phần tử trong mảng một lần.
-O(n2) (độ phức tạp thời gian bậc hai): Đây là loại thuật toán có thời gian thực thi tăng theo bình phương của kích thước đầu vào. Ví dụ: Thuật toán sắp xếp Bubble Sort, các thuật toán tìm kiếm không hiệu quả như Linear Search trong một mảng lồng nhau.
-O(nk) (độ phức tạp thời gian bậc k): Đây là loại thuật toán có thời gian thực thi tăng theo lũy thừa của kích thước đầu
QT
Quoc Tran Anh Le
Giáo viên
9 tháng 11 2023
1. Tính số lần lặp của vòng lặp bên trong của thuật toán sắp xếp chèn tuyến tính.
2. Tính số lần lặp của vòng lặp ngoài của thuật toán sắp xếp chèn tuyến tính.
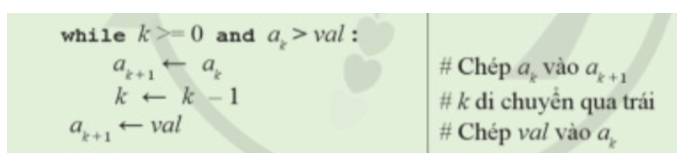
3. Ước lượng độ phức tạp thời gian của thuật toán sắp xếp chèn tuyến tính:
Vòng lặp for bên ngoài kiểm soát việc thực hiện đúng n-1 bước.
Vòng lặp while lồng bên trong thực hiện đồng thời cùng lúc hai việc a) và b) theo cách dịch chuyển dần từng bước sang trái, từ vị trí i tới vị trí k+1
LD
25 tháng 4
tính E(300)=300/log2(300), E(90000)=90000/log2(90000)
Vì độ hiệu quả tỉ lệ thuận với thời gian thực hiện
nên ta có tỉ số 0,02/E(300)=x/E(90000) (x là giá trị cần tìm).
Từ đó tính được x=3
QT
Quoc Tran Anh Le
Giáo viên
23 tháng 8 2023
Số lần so sánh giữa các phần tử: Trong thuật toán sắp xếp chọn, số lần so sánh giữa các phần tử là cố định, không phụ thuộc vào dữ liệu đầu vào. Cụ thể, số lần so sánh trong thuật toán sắp xếp chọn là \(\dfrac{n\left(n-1\right)}{2}\), với n là số phần tử trong mảng hoặc danh sách.
Số lần hoán đổi giữa các phần tử: Trong thuật toán sắp xếp chọn, số lần hoán đổi giữa các phần tử có thể đạt đến tối đa n-1 lần, với n là số phần tử trong mảng hoặc danh sách.
Vậy độ phức tạp thời gian của thuật toán sắp xếp chọn là O(n2), hay \(\dfrac{n\left(n-1\right)}{2}\) lần so sánh và tối đa n-1 lần hoán đổi giữa các phần tử.
QT
Quoc Tran Anh Le
Giáo viên
23 tháng 8 2023
Các tiêu chí đánh giá tính hiệu quả của thuật toán hay chương trình giải một bài toán có thể khác nhau tùy vào mục đích và yêu cầu của dự án hoặc ứng dụng cụ thể. Dưới đây là một số thảo luận về các tiêu chí được đưa ra trong câu hỏi:
1. Tiêu chí thời gian chạy (runtime): Thời gian chạy của chương trình là một yếu tố quan trọng trong đánh giá tính hiệu quả của thuật toán hay chương trình. Nếu chương trình chạy nhanh, đáp ứng được yêu cầu về thời gian đối với ứng dụng cụ thể, thì đây là một tiêu chí quan trọng để đánh giá tính hiệu quả của chương trình.
2. Tiêu chí tiết kiệm bộ nhớ: Việc sử dụng bộ nhớ của chương trình cũng là một yếu tố quan trọng trong đánh giá tính hiệu quả của chương trình, đặc biệt là đối với các ứng dụng có yêu cầu về tài nguyên hạn chế. Nếu chương trình sử dụng ít bộ nhớ và đáp ứng được yêu cầu về tài nguyên, thì tiêu chí này cũng được coi là quan trọng.
3. Tiêu chí đơn giản, rõ ràng, dễ hiểu: Độ đơn giản, rõ ràng và dễ hiểu của chương trình cũng là một yếu tố quan trọng trong đánh giá tính hiệu quả của chương trình, đặc biệt là trong việc duy trì và phát triển sau này. Nếu chương trình được viết một cách đơn giản, rõ ràng và dễ hiểu, thì nó sẽ dễ dàng trong việc duy trì, nâng cấp, và áp dụng cho các tình huống khác nhau.
Tham khảo:
QT1. Quy tắc cộng: O(f(n)+g(n))=O(max(f(n),g(n)))
QT2. Quy tắc nhân:
- Với hằng sô: O(C.f(n))=O(f(n))
- Với hàm số: O(f(n).g(n))=O(f(n)).O(g(n))