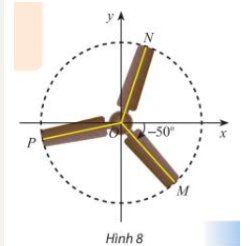
Trong Hình 8, chiếc quạt có ba cánh được phân bố đều nhau. Viết công thức tổng quát số đo của góc lượng giác (Ox,ON) và (Ox,OP).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì mâm bánh xe ô tô được chia thành năm phần bằng nhau nên mỗi phần có số đo bằng \(\dfrac{360^o}{5}=72^o\)
Ta có: \(\left(ON,OM\right)=\left(ON,Ox\right)+\left(Ox,OM\right)\\ \Rightarrow\left(ON,Ox\right)=99^o\)
Công thức số đo tổng quát của góc lượng giác \(\left(ON,Ox\right)=99^o+k\cdot360^o,k\in Z\)

a, Số đo của góc lượng giác (OM, ON) trong Hình 6 là \(60^o\)
b, Số đo của góc lượng giác (OM, ON) trong Hình 6 là \(60^o+2\cdot360^o=780^o\)
c, Số đo của góc lượng giác (OM, ON) trong Hình 6 là \(\dfrac{5}{6}\cdot\left(-360^o\right)=-300^o\)
Công thức tổng quát của số đo góc lượng giác (OM, ON) \(=60^o+360^o\cdot k,k\in Z\)

Ta có: \(\left(OA,OM\right)=120^o+k\cdot360^o,k\in Z\\ \left(OA,ON\right)=-75^o+k\cdot360^o,k\in Z\)

Bạn thông cảm, mình chưa biết vẽ hình trên máy tính nên mình chỉ ghi chữ thôi nhé
a) vì Ox,Oy,Oz cùng thuộc một nửa mặt phẳng bờ là tia Ox và góc xOy < góc xOz (30°<120°) nên tia Oy nằm giữa hai tia Ox và Oz
b) vì tia Oy nằm giữa hai tia Ox và Oz nên:
xOy+yoz=xOz
Thay số vào ta có: 30°+yOz=120°
yOz=120°_30°= 90°
c) vì Om là tia phân giác của xOy nên Om nằm giữa Ox và Oy
và xOm=mOy=xoy/2=30°/2=15°
Vì On là tia phân giác của yOz nên On nằm giữa Oy và Oz
và yOn=nOz=yOz/2=120°/2=60°
Vì tia Oy nằm giữa hai tia Ox và Oz
Tia Om nằm giữa hai tia Ox và Oy
Tia On nằm giữa hai tia Oy và Oz thì tia Oy nằm giữa hai tia Om và On nên
mOy+yOn=mOn
Thay số vào ta có:15°+60°=mOn
15°+60°=75°
Vậy mOn=75°

Bài 2:
a: Ta có: Ox là tia phân giác của \(\widehat{mOn}\)
nên \(\widehat{mOx}=\widehat{nOx}=\dfrac{180^0}{2}=90^0\)
b: Ta có: Oy là tia phân giác của \(\widehat{mOx}\)
nên \(\widehat{yOx}=\dfrac{90^0}{2}=45^0\left(1\right)\)
Ta có: tia Ot là tia phân giác của \(\widehat{nOx}\)
nên \(\widehat{xOt}=\dfrac{90^0}{2}=45^0\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra \(\widehat{xOy}=\widehat{xOt}\)
Công thức tổng quát số đo của góc lượng giác \(\left(Ox,ON\right)=70^o+k\cdot360,k\in Z\)
Công thức tổng quát số đo của lượng giác
\(\left(Ox,OP\right)=\left(Ox,OM\right)+\left(OM,OP\right)=-50-120^o+m\cdot360^o=-170^o+m\cdot360^o,m\in Z\)