Có thể sử dụng mối liên hệ giữa dao động điều hoà và chuyển động tròn đều để xác định pha ban đầu, thời gian để vật đi từ điểm này đến điểm khác trong dao động điều hoà được không?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chu kì dao động là: \(T=\dfrac{1}{f}=\dfrac{1}{5}=0,2\left(s\right)\)
Tần số góc của dao động là: \(\omega=2\pi f=10\pi\left(rad/s\right)\)
Lúc t = 0, ta có: \(\left\{{}\begin{matrix}x=A\\v=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}cos\varphi=1\\sin\varphi=0\end{matrix}\right.\Rightarrow\varphi=0\)
Phương trình dao động là: \(x=10cos\left(10\pi t\right)cm\)
Vẽ đồ thị:
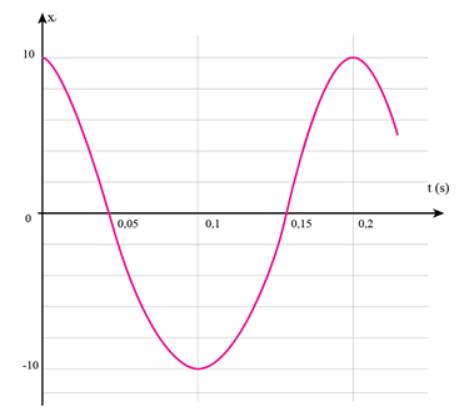

Đáp án D
Vòng tròn đơn vị:
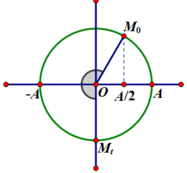
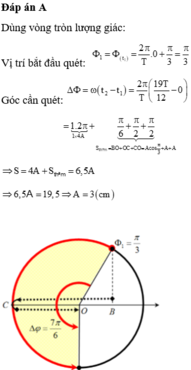
Thời điểm ban đầu vật ở vị trí M0 (hình vẽ), li độ của vật x = A / 2 . Sau thời gian 7T/12 ứng với góc quét 210 ° như hình vẽ, vật đến VTCB ở Mt.
Quãng đường vật đi được: s = A / 2 + A + A = 2 , 5 A = 10 = > A = 4 ( c m ) .

Đáp án D

Một vật dao động điều hòa phải mất 0,25s để đi từ điểm có vận tốc bằng không tới điểm tiếp theo cũng như vậy ⇒ khoảng thời gian này tương ứng vật chuyển động giữa hai vị trí biên:
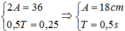
Tốc độ trung bình:
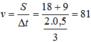
STUDY TIP
Tốc độ trung bình của vật: v = S ∆ t
Vận tốc trung bình của vật: v T B = x 2 - x 1 ∆ t
Cần phân biệt tốc độ trung bình và vận tốc trung bình; vận tốc trung bình có giá trị đại số

Đáp án B
Phương trình dao động của vật 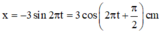
Do đó pha ban đầu của dao động là ![]()
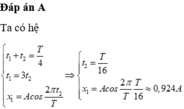
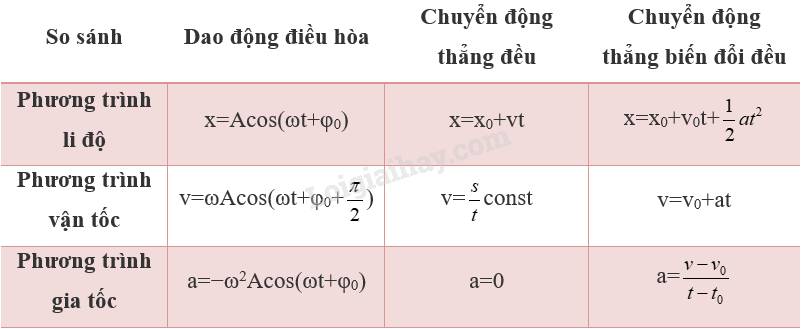
2. Vật chuyển động tròn đều trên quĩ đạo thì có hình chiếu xuống một đường kính của quĩ đạo là dao động điều hòa. Do đó một dao động điều hòa có dạng
x = A cos(ωt+φ) có thể được biểu diễn tương đương với một chuyển động tròn đều nếu có:
- Tâm của đường tròn là VTCB 0
- Bán kính của đường tròn bằng với biên đọ dao động R = A
- Thời gian để chất điểm quay hết một vòng là một chu kì T
- Chiều quay của vật ngược chiều kim đồng hồ
- Góc mà bán kính nối vật chuyển động quét được trong quá trình vật chuyển động tròn đều Δφ = ωΔt