Cho hình bình hành MNPQ gọi a b c d lần lượt là trung điểm các cạnh MN NP QM Tứ giác ABCD là hình gì vì sao
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
S
13 tháng 10 2018
tự vẽ hình
nối MP
Xét t/g MNP có: AM=AN(gt),BN=BP(gt)
=>AB là đường tb của t/g MNP
=>AB//MP và AB=1/2MP (1)
Xét t/g MQP có: MD=DQ(gt),QC=CP(gt)
=>CD là đường tb của t/g MQP
=.CD//MP và CD=1/2MP(2)
Từ (1) và (2) => AB=CD (3)
Lại có:AB//MP, CD//MP
=>AB//CD (4)
Từ (3)và (4) => tứ giác ABCD là HBH
7 tháng 10 2021
Xét ΔMQN có
E là trung điểm của MN
H là trung điểm của MQ
Do đó: EH là đường trung bình của ΔMQN
Suy ra: EH//NQ và \(EH=\dfrac{NQ}{2}\left(1\right)\)
Xét ΔQPN có
F là trung điểm của NP
G là trung điểm của GP
Do đó: FG là đường trung bình của ΔQPN
Suy ra: FG//NQ và \(FG=\dfrac{NQ}{2}\left(2\right)\)
Từ (1)và (2) suy ra EH//GF và EH=GF
hay EHGF là hình bình hành
30 tháng 11 2018
Bạn tự vẽ hình nha
Xét tam giác MNP có :
D là trung điểm MN ( GT )
E là trung điểm MP ( GT )
=> DE là đường trung bình của tam giác MNP
=> DE = NP/2 (1)
CMTT : DG = MQ/2 (2)
và FG = NP/2 (3)
và EF =MQ/2 (4)
Từ (1), (2), (3), (4), Mà NP = MQ ( GT )
=> DE = EF = FG= GD
Xét tứ giác DEFG có :
DE = EF = FG= GD ( CMT )
=> DEFG là hình thoi
Vậy DEFG là hình thoi
Bạn tự vẽ hình nha
Câu b)
Xét tam giác MNP có :
D là trung điểm MN ( GT )
E là trung điểm MP ( GT )
=> DE là đường trung bình của tam giác MNP
=> DE // NP
CMTT : DG // MQ
Để hình thoi DEFG là hình vuông
<=> góc GDE = 90 độ
<=> GD vuông góc DE
Ta có : DE // NP ( CMT )
và DG// MQ ( CMT )
Để GD vuông góc DE
<=> MQ vuông góc NP
Vậy tứ giác MNPQ có NP = MQ, NP vuông góc MQ thì tứ giác DEFG là hình vuông
G
29 tháng 10 2021
Xét ΔMQN có
E là trung điểm của MN
H là trung điểm của MQ
Do đó: EH là đường trung bình của ΔMQN
Suy ra: EH//NQ và \(EH=\frac{NQ}{2}\left(1\right)\)
Xét ΔQPN có
F là trung điểm của NP
G là trung điểm của GP
Do đó: FG là đường trung bình của ΔQPN
Suy ra: FG//NQ và\(FG=\frac{NQ}{2}\left(2\right)\)
Từ (1)và (2) suy ra EH//GF và EH=GF
hay EHGF là hình bình hành
29 tháng 10 2021
Giải
Nối M với P và nối N với Q
Xét tam giác QMP có: \(\left \{ {{\text{H là trung điểm QM (gt)}} \atop {\text{G là trung điểm QP (gt)}}} \right.\)
Do đó HG là đường trung bình của tam giác QMP
\(\Rightarrow HG//MP\left(1\right)\)
Xét tam giác MNP có: \(\left \{ {{\text{E là trung điểm MN (gt)}} \atop {\text{F là trung điểm NP (gt)}}} \right.\)
Do đó EF là đường trung bình của tam giác MNP
\(\Rightarrow EF//MP\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\Rightarrow HG//EF\left(3\right)\)
Xét tam giác MNQ có: \(\left \{ {{\text{H là trung điểm QM (gt)}} \atop {\text{E là trung điểm MN (gt)}}} \right.\)
Do đó HE là đường trung bình của tam giác MNQ
\(\Rightarrow HE//NQ\left(4\right)\)
Xét tam giác NQP có: \(\left \{ {{\text{G là trung điểm QP (gt)}} \atop {\text{F là trung điểm NP (gt)}}} \right.\)
Do đó GF là đường trung bình của tam giác NQP
\(\Rightarrow GF//QN\left(5\right)\)
Từ \(\left(4\right);\left(5\right)\Rightarrow HE//GF\left(6\right)\)
Từ \(\left(3\right);\left(6\right)\Rightarrow\)Tứ giác EFGH là hình bình hành
Vậy tứ giác EFGH là hình bình hành
CM
25 tháng 1 2018
Đáp án B
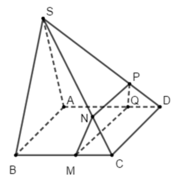
Ta có: MN // BS ⇒ C M C B = C N C S
MQ // CD // AB (do ABCD là hình bình hành nên AB //CD) ⇒ C M C B = D Q D A
NP // CD ⇒ C N C S = D P D S
Do đó: D P D S = D Q D A PQ // SA (Định lý Ta - lét trong tam giác SAD)
Lại có MN // BS và SB ∩ SA = S
Do đó MN không thể song song với PQ
Xét tứ giác MNPQ có NP // MQ (//CD)
Do đó MNPQ là hình thang.
Vậy khẳng địn (1) và (3) đúng.
Đáp án B
Sửa đề: A,B,C,D lần lượt là trung điểm của MN,NP,PQ,MQ
Xét ΔNMP có NA/NM=NB/NP
nên AB//MP và BA/MP=NA/NM=1/2
Xét ΔQMP có QC/QP=QD/QM=1/2
nên DC//MP và DC=1/2MP
=>AB//CD và AB=CD
=>ABCD là hình bình hành