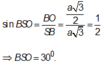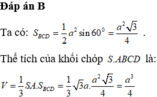cho hình chóp S.ABCD có đáy là hình thoi cạnh a .canh ben SA vuong goc với mp day va SA =a .biet goc giua mpSBCvà ABCD=60 tinh the tich hinh chop S.ABCD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, xét tam giác ABC , AB vuông góc BC =>AC= can AB2+-BC2 =>AC= can 800 =>AC=20 can 2 cm => AO = 1/2AC=1/2.20 căn 2=10 căn 2 cm Sét tam giác SOA , SỐ vuông góc AO => SO = can SA2-AO2 = 242- ( 10 căn 2 )2 = 19,4 cm
Tiếp câu a , thể tích của hình chóp đều S.ABCD là :V=1/3.S.h => Sđáy = 20²=400cm² => V=1/3.400.19'4=2586,7 cm3

\(\begin{cases}\left(SBC\right)\perp\left(ABCD\right)\\SH\perp CB\\\left(SBC\right)\cap\left(ABCD\right)=AB\end{cases}\Rightarrow SH\perp\left(ABCD\right)}\)

Đáp án là C.
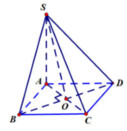
Ta có: S A B C = 1 2 B A . B C . sin A B C ⏞ = 1 2 a . a . sin 60 0 = a 2 3 4 ⇒ S A B C D = 2 S A B C = a 2 3 2 .
Thể tích của khối chóp S.BCD là:
V S . B C D = 1 3 S A . S B C D = 1 3 S A . 1 2 S A B C D = 1 3 . A = a 3 . a 2 3 2 = a 8 2 .

Đáp án C

Gọi E và H lần lượt là hình chiếu của A lên CB và SE
Ta có: A E = A B sin A B E ^ = s i n 60 ° = a 3 2
A H = A E sin 60 ° = 3 2 a . 3 2 = 3 a 4

Chọn B.
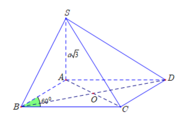
Gọi O = AC ∩ BD. Vì ABCD là hình thoi nên BO ⊥ AC(1). Lại do:
![]()
Từ (1) và (2) ta có:BO ⊥ (SAC)
![]()
Ta có: ![]()
Vì ABCD là hình thoi có ABC = 60 ° nên tam giác ABC đều cạnh a
![]()
Trong tam giác vuông SBO ta có: