Cho tam giác ABC nhọn vẽ đường tròn đường kính BC cắt AB và AC tại E và F. a, Tính gócBEC và BFC. b, Gọi H là giao của BFvà CE. Chứng minh AH vuông góc với BC. c, từ B kẻ đường cao vuông góc với EF t...

NT

Nguyễn Thị Phương Thúy

1 tháng 7 2023 - olm

Cho tam giác ABC nhọn vẽ đường tròn đường kính BC cắt AB và AC tại E và F. a, Tính gócBEC và BFC. b, Gọi H là giao của BFvà CE. Chứng minh AH vuông góc với BC. c, từ B kẻ đường cao vuông góc với EF tại M, từ C Kẻ đường vuông góc EF tại N. chứng minh EM = FN Giúp mik với! Mik đang cần gấp:( Cảm ơn mn nhiều ạ!! (vẽ cả...

Đọc tiếp

#Toán lớp 9

0

YB

Yến Bùi Đoàn Hải

12 tháng 5 2015 - olm

cho tam giác ABC có ba góc nhọn .Đường tròn tâm O đường kính BC cắt AB, AC lần lượt tại E và D. gọi giao điểm của CE và BD là H

a) chứng minh tứ giác AEHD nội tiếp

b) kẻ AF vuông góc với BC tại F. Chứng minh A, H, F thẳng hàng

c) đường thẳng EF cắt đường tròn tại điểm thứ 2 là K. chứng minh DK// AF

#Toán lớp 9

1

TN

Thắng Nguyễn

9 tháng 8 2016

cho tam giác ABC vuông cân tại B.Trên cạnh BA và BC lấy hai điểm E và F sao cho BE = BF.Qua B và E kẻ đường vuông góc với AF,chúng cắt AC lần lượt ở I và K. EK cắt BC tại H
a)Chứng minh tam giác AHC cân
b)chứng minh I là trung điểm KC
c)Gọi M,N,P lần lượt là trung điểm EC,AF,EF

Đúng(0)

DT

Diệu Trần Thị Huyền

3 tháng 5 2023

CM CÂU C THÔI NHÁcho tam giác abc nhọn, đường tròn (O) đường kính bc cắt ab, ac lần lượt tại E và f. gọi h là giao điểm của bf và ce, ah cắt bc tại d. a) chứng minh ah vuông góc với bc và tứ giác aehf nội tiếp, xác định tâm K của đường tròn này. b) chứng minh ke là tiếp tuyến của đường tròn (O) và năm điểm o, d, e, k, f cùng thuộc một đường tròn c) qua h vẽ đường thẳng vuông góc ho cắt ab, ac lần lượt tại...

Đọc tiếp

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

11 tháng 5 2023

c: Theo câu b, ta được: H là tâm đường tròn ngoại tiếp ngũ giác DEKFO

OH vuông góc MN

=>MN là đường kính của (H)

=>HM=HN

Đúng(0)

HT

Hoàn Trần

2 tháng 8 2023

Cho tam giác nhọn ABC (AB<AC). Đường tròn (O) đường kính BC cắt AB và AC lần lượt tại E và D. Gọi H là giao điểm của BD và CE. Tia AH cắt BC tại F,a) Chứng minh AF vuông góc với BC và tứ giác BEHF nội tiếpb) Gọi M là trung điểm của CH. Chứng minh tứ giác OMEF nội tiếpc) DF cắt Ce tại N. Qua N kẻ đường thẳng vuông góc với CE cắt BC và BD lần lượt tại I và K. Chứng minh N là trung điểm của...

Đọc tiếp

#Toán lớp 10

1

NL

Nguyễn Lê Phước Thịnh

2 tháng 8 2023

a: Xét (O) có

góc BEC, góc BDC đều là các góc nội tiếp chắn nửa đường tròn

=>góc BEC=góc BDC=90 độ

=>CE vuông góc AB, BD vuông góc AC

Xét ΔABC có

CE,BD là đường cao

CE cắt BD tại H

=>H là trực tâm

=>AH vuông góc BC tại F

góc BEH+góc BFH=180 độ

=>BEHF nội tiếp
b: Xét ΔHCB có CO/CB=CM/CH

nên OM//BH

=>góc COM=góc CBH

=>góc COM=góc FEC

=>góc MOF+góc FEM=180 độ

=>OMEF nội tiếp

Đúng(0)

VQ

VõThị Quỳnh Giang _

24 tháng 3 2020 - olm

1 . Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường tròn tâm I, đường kính AH cắt AB, AC lần lượt tại M và N, D là giao điểm của MN và OAa) chứng minh AM.AB=AN.AC và tứ giác BMNC nội tiếpb) cm tam giác ADI đồng dạng tam giác AHOc) gọi E là giao điểm BC và NM, K là giao điểm AE và (I). cm góc BKC = 90°2 . Cho tam giác ABC nhọn, BC = AC, đường tròn tâm O đường kính BC cắt AB,AC tại E,F. BF cắt CE tại...

Đọc tiếp

#Toán lớp 9

1

H2

•๖ۣۜHυүềη ²ƙ⁷ ( ๖ۣۜTεαм ๖ۣۜBạ¢ɦ ๖ۣۜ...

26 tháng 3 2020

ối chồi em mới lớp 7 thôi

Đúng(0)

MT

Minh Thư LêThị

27 tháng 12 2017 - olm

Cho tam giác ABC nội tiếp trong đường tròn (O). Biết AB=4cm, BC=8,5cm và CA=7,5cm. Kẻ dây AD vuông góc với BC. Gọi E là giao điểm của DB và CA. Qua E kẻ đường thẳng vuông góc với BC, cắt BC ở H, cắt AB ở F.a) Chứng minh tam giác ABC vuông và tính độ dài đường cao vẽ từ đỉnh góc vuông của tam giác ABC.b) Chứng minh rằng EF=2AH.c) Chứng minh rằng HA là tiếp tuyến của đường tròn...

Đọc tiếp

#Toán lớp 9

0

NQ

Nguyễn Quang Trường

19 tháng 12 2019 - olm

Cho tam giác nhọn ABC nội tiếp đường tròn (O). Kẻ đường cao AH, đường kính AD.Kẻ HE vuông góc với AB tại E, HF vuông góc với AC tại F . Gọi G là giao điểm của BF và CE . BF và CE cắt đường tròn tại M và N. Chứng minh MN vuông góc với AD

#Toán lớp 9

0

CT

Cố Tử Thần

7 tháng 4 2019 - olm

Cho đường tròn (O), đường kính BC. Lấy 1 điểm A trên đường tròn (O) sao cho AB>AC. Từ A kẻ AH vuông góc vs BC( H thuộc BC). Từ H vẽ HE vuông góc với AB và HF vuông góc với AC (E thuộc AB và F thuộc AC).a, chứng minh rằng AEHF là hình chữ nhật và OA vuông góc với EFb, Đường thẳng EF cắt đường tròn tại P và Q (E nằm giữa P và F)Chứng minh AP^2=AE*AB. suy ra APH là tam giác cânc, Gọi D là giao điểm...

Đọc tiếp

#Toán lớp 9

0

PT

Pham Trong Bach

17 tháng 2 2018

Cho tam giác nhọn ABC (AB < AC). Đường tròn tâm O đường kính BC cắt AB và AC lần lượt tại E và D. Gọi H là giao điểm của BD và CE; AH cắt BC tại I.

a) Chứng minh AI vuông góc với BC và EC là phân giác của góc IED.

#Toán lớp 9

1

CM

Cao Minh Tâm

17 tháng 2 2018

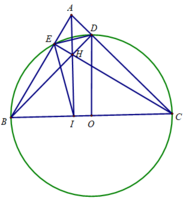
Đề kiểm tra Toán 9 | Đề thi Toán 9

a) Chứng minh AI BC

Ta có ∠BEC = BDC = 90 0 (hai góc nội tiếp chắn nửa đườn tròn)

Đúng(0)

TT

Thảo Thanh

18 tháng 4 2023

Cho tam giác nhọn ABC , đường tròn tâm O đường kính BC cắt AC và AB lần lượt tại E và F,BE và CF cắt nhau tại H. a. C/m: góc BFC=90°;AH vuông góc với BC tại D và AFHE là tứ giác nội tiếp b. Gọi I,K lần lượt là trung điểm của BF và CE. C/m AH.AD=AF.AB và IDOK nội tiếp

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

19 tháng 4 2023

a: góc BFC=góc BEC=1/2*180=90 độ

Xét ΔABC có

BE,CF là đường cao

BE cắt CF tại H

=>H là trực tâm

=>AH vuông góc BC

góc AFH+góc AEH=180 độ

=>AEHF là tứ giác nội tiếp

b: Xét ΔAFH vuông tại F và ΔADB vuông tại D có

góc FAH chung

=>ΔAFH đồng dạng với ΔADB

=>AF/AD=AH/AB

=>AF*AB=AD*AH

Đúng(1)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP