Cho tam giác ABC có AB = 6,AC = 8 và hai đường trung tuyến BM,CN vuông góc với nhau. Tính độ dài cạnh BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
LL
loan lê
30 tháng 6 2023
Đúng(3)
Những câu hỏi liên quan
GH
19 tháng 6 2023
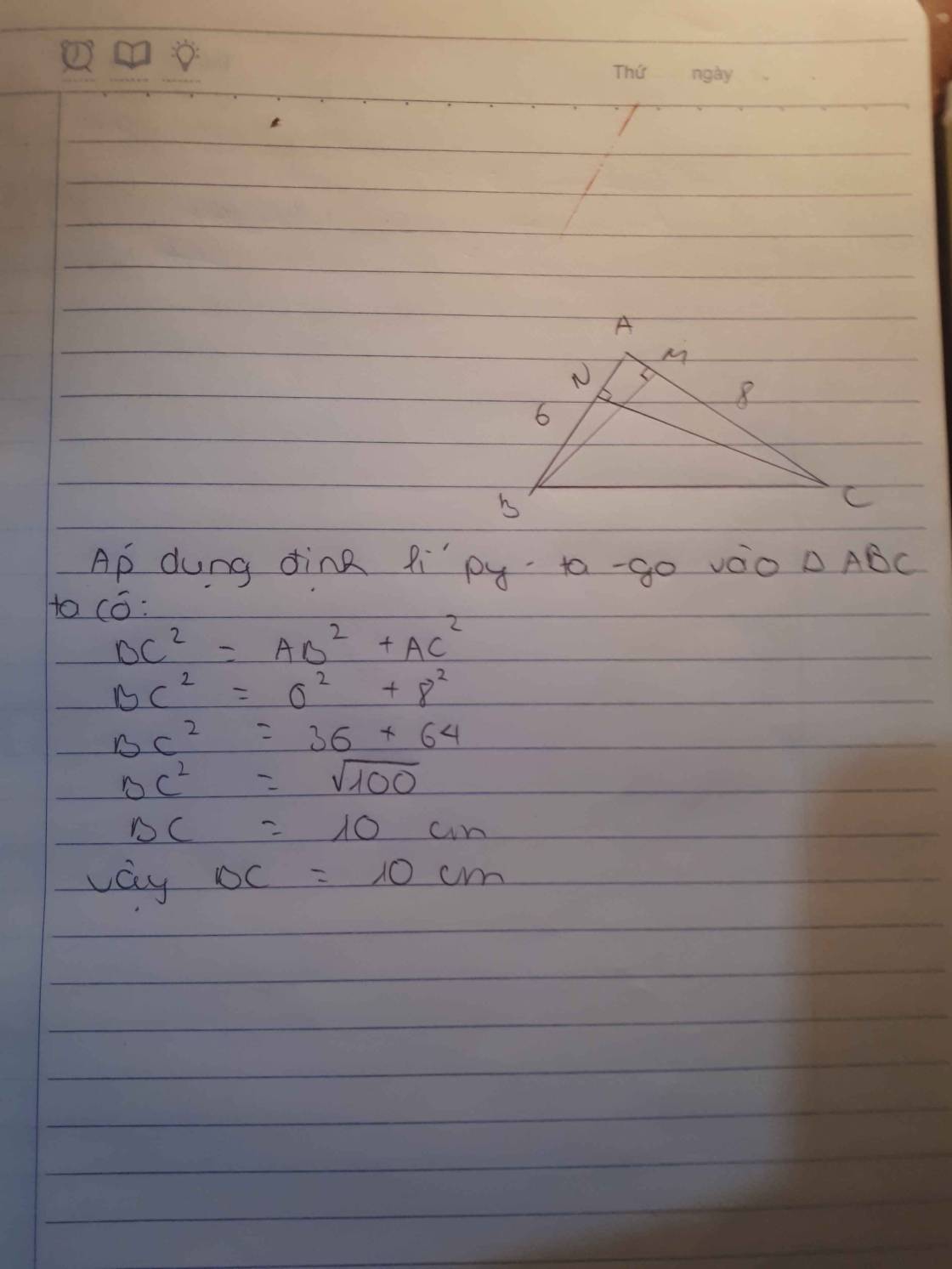
a)
Có 2 trung tuyến BN, CM cắt nhau suy ra \(BN\perp AM\)
Gọi G là trọng tâm tam giác ABC, ta có \(BG=\dfrac{2}{3}BN=\dfrac{2}{3}.4=\dfrac{8}{3}\left(cm\right)\)
Trong tam giác ABN vuông tại A, đường cao AG, ta có:
\(AB^2=BG.BN\) (hệ thức lượng)
\(\Rightarrow AB=\sqrt{\dfrac{8}{3}.4}=\dfrac{4\sqrt{6}}{3}\left(cm\right)\)
Tam giác ABN vuông tại A
\(\Rightarrow AN^2=BN^2-AB^2\\ \Rightarrow AN=\sqrt{4^2-\left(\dfrac{4\sqrt{6}}{3}\right)^2}=\dfrac{4\sqrt{3}}{3}\left(cm\right)\)
Mà N là trung điểm AC => AC = \(\dfrac{8\sqrt{3}}{3}\left(cm\right)\)
Áp dụng đl pytago vào tam giác ABC:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{\left(\dfrac{4\sqrt{6}}{3}\right)^2+\left(\dfrac{8\sqrt{3}}{3}\right)^2}=4\sqrt{2}\left(cm\right)\)
Thừa dữ kiện AM = 3cm, bạn coi kỹ đề đủ/ đúng hết chưa thì cmt để chút mình coi lại bài giải
28 tháng 11 2016
Dùng hình bạn Ngọc nhé (khỏe khỏi phải vẽ :)
Xét \(\Delta BOC\)và \(\Delta NBC\)có
\(\widehat{OCB}\)chung
\(\widehat{BOC}=\widehat{NBC}=90\)
\(\Rightarrow\Delta BOC\)đồng dạng \(\Delta NBC\)
\(\Rightarrow\frac{BC}{NC}=\frac{OC}{BC}\Leftrightarrow BC^2=NC.OC\)
\(\Leftrightarrow BC^2=NC.\frac{2}{3}NC=\frac{2NC^2}{3}\)(Vì O là trọng tâm)
\(\Rightarrow NC=\sqrt{\frac{3}{2}}BC=\frac{\sqrt{3}.20132014}{\sqrt{2}}\)
LT
2
10 tháng 11 2016
Goi G là giao điểm của 2 đường trung tuyến CE và BD ta có GD = 1/2 BG và EG = 1/2 CG [Vì theo tính chất của trung tuyến tại giao điểm G, của 3 đường ta có G chia đường trung tuyến ra làm 2 phần, phần này gấp đôi phần kia.]
Áp dụng định lý pythagore vào tam giác vuông BGE ta có:
BG^2 = EB^2 - EG^2 = 9 - EG^2 = 9 - (1/2. GC)^2 (1)
Áp dụng định lý pythagore vào tam giác vuông CGD ta có:
GC^2 = CD^2 - GD^2 = 16 - GD^2 = 16 - (1/2BG)^2 (2)
mặt khác BC^2 = BG^2 + GC^2. Do đó từ (1) và (2) ta có:
BC^2 = 9 -1/4 GC^2 + 16 - 1/4 BG^2 = 25 - 1/4(GC^2 + BG^2)
<=> BC^2 + 1/4(GC^2 + BG^2) = 25 <=> BC^2 + 1/4BC^2 = 25 <=> 5/4BC^2 = 25 <=>
BC^2 =25. 4/5 = BC^2 =20 <=> BC = căn 20 <=>
BC = 2.(căn 5) cm