Bài 22: a.Cho hình chữ nhật ABCD có AB = 6, BC = 8. Tính độ dài đường chéo AC
b. Hai đường chéo AC và BD cắt nhau tại trung điểm O. Chứng minh OA = OB = OC = OD
c. Tam giác ABC vuông tại B có trung tuyến BO = … AC
Bài 24: Cho đoạn thẳng AB. M là trung điểm của đoạn thẳng AB. Từ M kẻ đường thẳng d vuông góc với AB. O là điểm bất kỳ trên d.
Chứng minh ∆OMA = OMB . Từ đó suy ra OA = OB
Bài 25: Điển vào chỗ trống
Nếu M nằm trên đường trung trực của đoạn thẳng AB thì MA = …
Nếu MA = MB thì M nằm trên đường … của đoạn thẳng AB.
Giao điểm của 3 đường trung trực trong tam giác thì cách đều 3 đỉnh của tam giác. Giao điểm đó được gọi là tâm đường tròn ..
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABH vuông tại H và ΔACB vuông tại B có
\(\widehat{BAH}\) chung
Do đó: ΔABH\(\sim\)ΔACB

a. Xét ΔABH và ΔACB có
∠A chung
∠AHB = ∠ABC = 90
⇒Đpcm
b. AD định lý PYTAGO cho ΔABC ta tính đc AC=25 cm
vì ΔABH ∼ ΔACB ⇒ BH/BC = AB/AC
thay số vào và giải
c. câu c tự cm theo định lý Talet đảo
a: Xét ΔABH vuông tại H và ΔACB vuông tại B có
góc BAH chung
=>ΔABH đồng dạng với ΔACB
b: \(AC=\sqrt{7^2+24^2}=25\left(cm\right)\)
BH=7*24/25=6,72(cm)

a) Xét ΔANI và ΔCND có
\(\widehat{ANI}=\widehat{CND}\)(hai góc đối đỉnh)
\(\widehat{IAN}=\widehat{DCN}\left(=45^0\right)\)
Do đó: ΔANI\(\sim\)ΔCND(g-g)

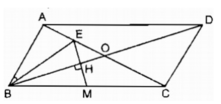
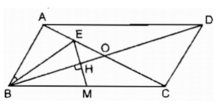
Vì ABCD là hình bình hành và E là trung điểm của AO (vì BE là trung tuyến của tam giác ABO) nên ta có: AO = CO = 1/2 AC; AE = 1/2 AO.
Mặt khác, theo giả thiết AC = 2AB nên dễ thấy AB = AO và do đó AE = 1/2AB
Xét hai tam giác AEB và ABC, ta có:
Góc A chung
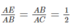
Vậy △ AEB đồng dạng △ ABC (c.g.c)
Suy ra: hai góc tương ứng bằng nhau ∠ ABE = ∠ ACB (đpcm)

Theo chứng minh ở câu a. △ AEB đồng dạng △ ABC theo tỉ số k = 1/2 nên dễ thấy BE = 1/2 BC hay BE = BM
Suy ra: ΔBEM cân tại B.
Xét tam giác EBC có: 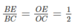
Suy ra: OB là đường phân giác góc EBC
BO là đường phân giác góc ở đỉnh của tam giác cân BEM nên BO vuông góc với cạnh đáy EM (đpcm).


24:
Xét ΔOMA vuông tại M và ΔOMB vuông tại M có
OM chung
MA=MB
=>ΔOMA=ΔOMB
=>OA=OB