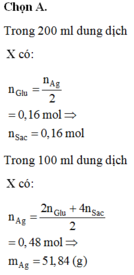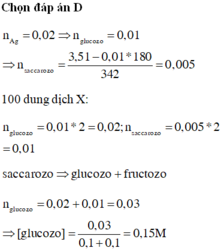Cần phải thêm bao nhiêu mL NH3 1M vào 10 mL dd AgNO3 0,1M để khi pha loãng thành 100 mL nồng độ tự do của ion Ag+ là 10-8. Phức của Ag+ và NH3 có logarit các hằng số bền tổng cộng lần lượt là 3,32 và 7,24.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
Hướng dẫn:

Trong môi trường kiềm cả glucozo và fructozo đều có phản ứng tráng gương:
C6H12O6 + 2AgNO3 + 3NH3 + H2O → C6H11O7NH4 + 2Ag + 2NH4NO3
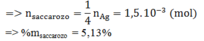

Đáp án : D
Glucozo -> 2Ag
=> nGlucozo = ½ nAg = 0,01 mol
=> CM(Glucozo) = 0,2M

Câu 3
Gọi V1,V2 lần lượt là thể tích của dd NaOH 3% và dd NaOH
10% cần dùng để pha chế dd NaOH 8%
Khối lượng dd NaOH 3% là 1,05.V1 (g)
- - > số mol của NaOH 3% là nNaOH = 1,05.V1.3/(100.40)
khối lượng dd NaOH 10% là 1,12.V2(g)
- - > Số mol của NaOH 10% là nNaOH = 1,12.V2.10/(100.40)
Khối lượng dd NaOH 8% là 2.1,11 = 2200(g)
- -> Số mol của NaOH 8% tạo thành là nNaOH
=2200.8/(100.40) = 4,4mol
Ta có hệ phương trình
{1,05V1 + 1,12V2 = 2200
{1,05.V1.3/(100.40) + 1,12.V2.10/(100.40) = 4,4
giải hệ này ta được
V1 = 598,6 (ml) ~0,6 (l)
V2 = 1403,06(ml) ~ 1,4 (l)

\(b.n_{NaOH\left(tổng\right)}=0,4.0,5+\dfrac{100.1,33.20\%}{40}=0,865\left(mol\right)\\ \left[Na^+\right]=\left[OH^-\right]=\left[NaOH\left(sau\right)\right]=\dfrac{0,865}{0,4+0,1}=1,73\left(M\right)\\ c.n_{HCl}=0,05.0,12=0,006\left(mol\right)\\ n_{HNO_3}=0,15.0,1=0,015\left(mol\right)\\ \left[H^+\right]=\dfrac{0,006+0,015}{0,05+0,15}=0,105\left(M\right)\\ \left[NO^-_3\right]=\dfrac{0,015}{0,05+0,15}=0,075\left(M\right)\\ \left[Cl^-\right]=\dfrac{0,006}{0,05+0,15}=0,03\left(M\right)\)
\(d.n_{H_2SO_4}=0,4.0,05=0,02\left(mol\right)\\ n_{HCl}=0,35.0,2=0,07\left(mol\right)\\ \left[H^+\right]=\dfrac{0,02.2+0,07}{0,05+0,35}=0,275\left(M\right)\\ \left[SO^{2-}_4\right]=\dfrac{0,02}{0,05+0,35}=0,05\left(M\right)\\ \left[Cl^-\right]=\dfrac{0,07}{0,05+0,35}=0,175\left(M\right)\\ f.n_{KOH}=\dfrac{20.1,31.32\%}{56}=\dfrac{131}{875}\left(mol\right)\\ n_{Ba\left(OH\right)_2}=0,08.1=0,08\left(mol\right)\\ \left[OH^-\right]=\dfrac{\dfrac{131}{875}+0,08.2}{0,02+0,08}=\dfrac{542}{175}\left(M\right)\\ \left[Ba^{2+}\right]=\dfrac{0,08}{0,02+0,08}=0,8\left(M\right)\)
\(\left[K^+\right]=\dfrac{\dfrac{131}{875}}{0,02+0,08}=\dfrac{262}{175}\left(M\right)\)