Cho hình lập phương ABCD A'B'C'D' có AB=BC=a AA'=a√3 tính A'C
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A.
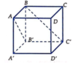
Đặt B ' 0 ; 0 ; 0 , A ' a ; 0 ; 0 , C ' 0 ; a ; 0 , B 0 ; 0 ; a ⇒ A a ; 0 ; a
Ta có B ' A → = a ; 0 ; a , B C ' → = 0 ; a ; − a , B ' B → = 0 ; 0 ; a
⇒ B ' A → , B C ' → = − a 2 ; a 2 ; a 2 ; B ' A → , B C ' → . B B ' → = a 3
d B ' A , B C ' = B ' A → , B C ' → . B B ' → B ' A → , B C ' → = a 3 3 a 4 = a 3 a 2 3 = a 3 3

THAM KHẢO:

a) Vì AA′⊥(ABCD) nên góc giữa đường thẳng AA' và (ABCD) là \(90^0\)
b) CC′⊥(ABCD) nên C là hình chiếu vuông góc của C' lên (ABCD).
Suy ra góc giữa BC' và (ABCD) là \(\widehat{C'BC}\)=\(45^O\) (Vì BCC'C' là hình vuông)c) Gọi cạnh của hình lập phương là a
Ta có: AC=\(a\sqrt{2}\),tan \(\widehat{ACA'}\)=\(\dfrac{1}{\sqrt{2}}\) nên \(\widehat{ACA'}\)=\(35^O\)
AA′⊥(ABCD) nên A là hình chiếu vuông góc của A' lên (ABCD)
Suy ra góc giữa A'C và (ABCD) là \(\widehat{ACA'}\)=\(35^O\)

Đáp án D
Gọi I là giao điểm của AC và BD
A I ⊥ B D A I ⊥ B B ' ⇒ A I ⊥ B B ' D ' D
=> B’I là hình chiếu vuông góc của AB’ lên (BB’D’D)
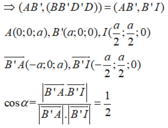

Đáp án D
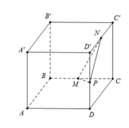
Chọn hệ trục tọa độ với
B 0 ; 0 ; 0 ; M 0 ; a ; 0 ; P a ; 2 a ; 3 a 2 v à N a 2 ; 2 a ; 3 a
Khi đó: M P → a ; a ; 3 a 2 ; M N → a 2 ; a ; 3 a
Do đó n M N P = → M P → ; M N → = a 2 3 2 ; − 9 4 ; 1 2
Suy ra
M N P : 6 x − 9 y + 2 z + 9 a = 0 ; A a ; 0 ; 0 .
Khi đó d A ; M N P = 6 a + 9 a 6 2 + 9 2 + 2 2 = 15 a 11 .
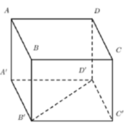




\(A'C'=\sqrt{a^2+a^2}=a\sqrt{2}\)
=>\(A'C=\sqrt{\left(a\sqrt{2}\right)^2+\left(a\sqrt{3}\right)^2}=a\sqrt{5}\)