Một miếng chì có khối lượng 1,5kg được nung nóng đến 190C rồi thả vào 1,5kg nước . Nhiệt độ khi có sự cân bằng là 30C .Biết nhiệt dung riêng của chì là 130J/kg.K, của nước là 4200J/kg.K Bỏ qua sự mất mát nhiệt cho môi trường xung quanh. Hãy tính
a) Nhiệt lượng do miếng chì tỏa ra
b) Độ tăng nhiệt độ của nước
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A
Ba miếng đồng, nhôm, chì có cùng khối lượng và ở cùng nhiệt độ. Nhiệt lượng của các miếng đồng, nhôm, chì thu vào tỉ lệ với nhiệt dung riêng mỗi chất nên c nhôm lớn nhất nên Q n lớn nhất, c chì bé nhất nên Q c bé nhất và ta có: Q n > Q đ > Q c

Gọi m1 là khối lượng của chì, m2 là khối lượng của kẽm, m là khối lượng của hợp kim:
m = m1 + m2 = 0,05kg (1)
Nhiệt lượng chì và kẽm tỏa ra:
Q1 = m1.c1.(t0 - t) = m1.130.(136 – 18) = 15340.m1
Q2 = m2.c2.(t0 - t) = m2.210.(136 – 18) = 24780.m2
Nhiệt lượng nước thu vào:
Qn = mn.cn.(t - tn) = 0,05.4200.(18 - 14) = 810J
Vì muốn cho nhiệt lượng kế nóng thêm lên 1oC thì cần 65,1J nên nhiệt lượng kế thu vào:
Q4 = Qk.(t – tn) = 65,1.(18 – 14) = 260,4J
Vì nhiệt lượng tỏa ra bằng nhiệt lượng thu vào nên: Q3 + Q4 = Q1 + Q2
↔ 15340.m1 + 24780.m2 = 1100,4 (2)
Từ (1), rút m2 = 0,05 – m1, thay vào phương trình (2), giải ra ta được:
m1 = 0,015kg, suy ra m2 = 0,035kg
Vậy khối lượng chì là 15 gam và khối lượng kẽm là 35 gam.

Nhiệt lượng do cả chì và đồng toả ra
\(Q_{tỏa}=Q_1+Q_2\\ \Leftrightarrow m_1c_1\Delta t+m_2c_2\Delta t\\ \Leftrightarrow0,2.130+0,2.380.\left(100-70\right)=3060J\)
Ta có pt cân bằng nhiệt
\(Q_{thu}=Q_{tỏa}=3060J\)

Độ lớn của nhiệt lượng toả ra và nhiệt lượng thu vào :
Q t o ả = c 1 m 1 t 2 - t + c 2 m 2 t 2 - t = c 1 m 1 t 2 - t + c 2 M - m 1 t 2 - t (1)
Q t h u = c m t - t 1 + c 0 m 0 t - t (2)
Từ (1) và (2) dễ dàng tính được :
m 1 = 0,104 kg = 104 g ; m 2 = 0,046 kg = 46 g.

a)Nhiệt lượng miếng đồng tỏa ra:
\(Q_{tỏa}=m_1c_1\left(t_1-t\right)=0,1\cdot380\cdot\left(100-60\right)=1520J\)
Cân bằng nhiệt: \(Q_{thu}=Q_{tỏa}\)
Nhiệt lượng nước thu vào: \(Q_{thu}=1520J\)
b)Nhiệt độ ban đầu của nước:
\(Q_{thu}=m_2c_2\left(t-t_2\right)=42,4\cdot10^{-3}\cdot4200\cdot\left(60-t_2\right)=1520\)
\(\Rightarrow t_2=51,46^oC\)

Gọi nhiệt độ cân bằng của hệ là \(t^oC\).
Nhiệt lượng đồng tỏa ra:
\(Q_{tỏa}=m_1c_1\left(t_1-t\right)=0,0008\cdot380\cdot\left(100-t\right)J\)
Nhiệt lượng nước thu vào:
\(Q_{thu}=m_2c_2\left(t-t_2\right)=1,5\cdot4200\cdot\left(t-50\right)J\)
Cân bằng nhiệt: \(Q_{thu}=Q_{tỏa}\)
\(\Rightarrow0,0008\cdot380\cdot\left(100-t\right)=1,5\cdot4200\cdot\left(t-50\right)\Rightarrow t=50,002^oC\)
a)Nhiệt độ của đồng ngay sau khi cân bằng nhiệt là:
\(t_1=100^oC-50,002^oC\approx50^oC\)
b)Nhiệt lượng nước thu vào:
\(Q_{thu}=1,5\cdot4200\cdot\left(50,002-50\right)=15,2J\)
c)Nước nóng thêm thêm \(\Delta t=50,002-50=0,002^oC\)

a) Nhiệt lượng thu vào của nước: Q = mcΔt = 4200.0,25.1,5 = 1575 J
b) Tính nhiệt dung riêng của chì:
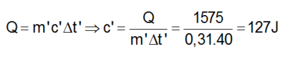
c) So với giá trị ghi ở bảng nhiệt dung riêng thì giá trị này bé hơn là do trong thí nghiệm, một lượng nhỏ nhiệt đã mất mát.


\(m_{chì}=1,5kg\)
\(t_2=190^oC;t_1=30^oC\)
\(\Rightarrow\Delta t=t_2-t_1=190-30=160^oC\)
\(c_{chì}=130J/kg.K\)
\(m_{nước}=1,5kg\)
\(c_{nước}=4200J/kg.K\)
\(a,Q_{tỏa}=?J\)
\(b,\Delta t=?^oC\)
======================
\(a,Q_{tỏa}=m.c.\Delta t=1,5.130.160=31200\left(J\right)\)
\(b,\) Cân bằng nhiệt :
\(Q_{thu}=Q_{tỏa}=31200\left(J\right)\)
\(\Leftrightarrow31200=1,5.4200.\Delta t\)
\(\Leftrightarrow\Delta t\approx4,95\left(^oC\right)\)