Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A.
Vận tốc của xe lúc bắt đầu hãm phanh
+ Ta có vận tốc; quãng đường trong chuyển động thẳng biến đổi đều
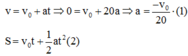
+ Thay (1) vào (2) ta được:
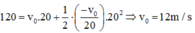
Do vậy, ta xác định được độ lớn động lượng của xe lúc bắt đầu hãm phanh bằng
p = m.v = 5000.12 = 60000 kg.m/s.
Chọn A.
Vận tốc của xe lúc bắt đầu hãm phanh
+ Ta có vận tốc; quãng đường trong chuyển động thẳng biến đổi đều
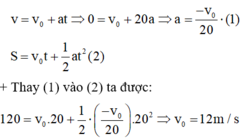
Do vậy, ta xác định được độ lớn động lượng của xe lúc bắt đầu hãm phanh bằng
p = m.v = 5000.12 = 60000 kg.m/s.
Đáp án C
Khi ô tô dùng hẳn thì
Quãng đường di chuyển của ô tô từ lúc hãm phanh đến khi dừng hẳn là
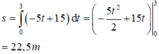
Ta có: \(v^2-v_0^2=2as\)
\(\Rightarrow a=\dfrac{v^2-v_0^2}{2s}=\dfrac{0^2-10^2}{2\cdot50}=-1\left(m/s^2\right)\)
Quãng đường mà vật di chuyển trong 4s kể từ lúc hãm phanh là:
\(s=v_0t+\dfrac{1}{2}at^2\)
\(\Rightarrow s=10\cdot4+\dfrac{1}{2}\cdot-1\cdot4^2=32\left(m\right)\)
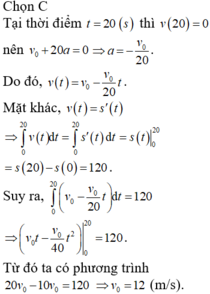
Ta có: \(s=\dfrac{1}{2}at^2=\dfrac{1}{2}a\cdot2^2\Rightarrow a=-5\left(\dfrac{m}{s^2}\right)\)
Lại có: \(v^2-v_0^2=2as\Rightarrow v_0=\sqrt{v^2-2as}\)
\(\Leftrightarrow v_0=\sqrt{0^2-2\cdot\left(-5\right)\cdot10}=10\left(\dfrac{m}{s}\right)\)
Động lượng xe lúc bắt đầu hãm phanh:
\(p=mv=5000\cdot10=50000\left(kg\cdot\dfrac{m}{s}\right)\)