Một hệ gồm hai vật có khôi lượng m1=1kg và m2=2kg chuyển động thẳng đều với tốc độ lần lượt là 3m/s và 2m/s theo hai hướng hợp nhau góc anpha 60 độ. Độ lớn của động lượng có giá trị là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
14 tháng 2 2020
m1=1kg; v1=3m/s⇒p1=m1.v1=3kgm/s; \(\overrightarrow{p1}\) cùng hướng với \(\overrightarrow{v1}\)
m2=3kg ;v2=1m/s⇒p2=m2.v2=3kgm/s; \(\overrightarrow{p2}\) cùng hướng với \(\overrightarrow{v2}\)
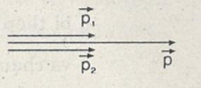
a) \(\overrightarrow{v1}\) và \(\overrightarrow{v2}\) cùng hướng:
\(p=p1+p2=6kgm/s\) \(\overrightarrow{p}\) cùng hướng với \(\overrightarrow{v1}\) và \(\overrightarrow{v2}\)
b) \(\overrightarrow{v1}\) và \(\overrightarrow{v2}\) ngược chiều
\(\overrightarrow{p}=0\)
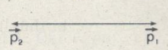c) \(\overrightarrow{v1}\) vuông góc với \(\overrightarrow{v2}\)
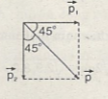\(p=p1.\sqrt{2}=3.\sqrt{2}\left(kgm/s\right)\)
\(\Rightarrow\overrightarrow{p}\) hợp với \(\overrightarrow{v1}\) và \(\overrightarrow{v2}\) cùng một góc 45 độ
d) \(\left(\overrightarrow{v1}'\overrightarrow{v2}\right)=120^o\)
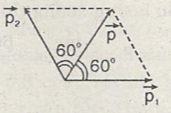
p = p1 = p2 = 3kgm/s.
\(\overrightarrow{p}\) hợp với \(\overrightarrow{v1}\) và \(\overrightarrow{v2}\) một góc 60 độ
1 tháng 3 2020
Động lượng của vật I:
\(\overrightarrow{p_1}=m_1\overrightarrow{v_1}\)
Động lượng của vật II:
\(\overrightarrow{p_2}=m_2\overrightarrow{v_2}\)
Động lượng của hệ:
\(\overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}=m_1\overrightarrow{v_1}+m_2\overrightarrow{v_2}\)
Vecto động lượng \(\overrightarrow{p}\) được xác định như hình vẽ.
Áp dụng hệ thức lượng trong tam giác thường, ta có:
\(\sqrt{p^2_1++p^2_2+2p_1p_2.cos60^o}=2,65kg.m\text{/}s\)
Chiếu hệ thức vecto \(\overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}\) xuống phương của \(\overrightarrow{p_2}\) , ta có:
\(p.cos\alpha=p_2+p_1.cos60^o\)
\(\Rightarrow cos\alpha=\frac{p_2+p_1.cos60^o}{p}=\frac{2+1.0,5}{2,65}=0,943\Rightarrow\alpha=39^o\)
Vậy vecto động lượng \(\overrightarrow{p}\) có độ lớn \(2,65kg.m\text{/}s\) và hợp lực với vận tốc \(\overrightarrow{v_2}\)một góc\(39^o\)
6 tháng 2 2021
Ta có : \(\left\{{}\begin{matrix}\overrightarrow{P_1}=m_1\overrightarrow{v_1}=2\overrightarrow{v_1}\\\overrightarrow{P_2}=m_2\overrightarrow{v_2}=3\overrightarrow{v_2}\end{matrix}\right.\)
Có : \(P=\sqrt{P_1^2+P_2^2+2P_1P_2Cos\left(\overrightarrow{P_1};\overrightarrow{P_2}\right)}\)
Lại có : Vecto P1 và P2 cùng phương với v1 và v2
Và \(\overrightarrow{v_1}.\overrightarrow{v_2}=v_1.v_2.cos\left(\overrightarrow{v1};\overrightarrow{v2}\right)\)
=> \(\left(\overrightarrow{P1};\overrightarrow{P2}\right)=45^o\)
\(\Rightarrow P=\sqrt{4v_1^2+9v^2_2+2.2.3\overrightarrow{v_1}\overrightarrow{v_2}.Cos45}=6\sqrt{7}\left(\dfrac{Kg.m}{s}\right)\)
19 tháng 4 2023
6 căn 7 mik bấm ra 15,8 trong khi đó mik tính lại lại ra 16,8 cơ
DQ
5 tháng 2 2021
Động lượng của vật \(m_1\) và vật \(m_2\) có độ lớn lần lượt là:
\(p_1=m_1v_1=0,2.20=4\) (kg.m/s)
\(p_2=m_2v=0,25.20=5\) (kg.m/s)
Trong trường hợp 2 vật chuyển động theo hai phương vuông góc thì:
\(p=\sqrt{p_1^2+p_2^2}=\sqrt{4^2+5^2}\approx6,4\) (kg.m/s)
\(\Rightarrow\) không có đáp án nào đúng.
17 tháng 4 2022
Động lượng vật thứ nhất:
\(p_1=m_1v_1=4m\) (g.m/s)
Động lượng vật thứ hai:
\(p_2=m_2v_2=3m\cdot3=9m\) (g.m/s)
Hai vật va chạm ngược chiều nhau. Bảo toàn động lượng:
\(\overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}\Rightarrow p=\left|p_1-p_2\right|=\left|4m-9m\right|=5m\)
Vận tốc của hai vật sau khi chuyển động là:
\(v=\dfrac{p}{m}=\dfrac{5m}{m_1+m_2}=\dfrac{5}{m+3m}=1,25\)m/s
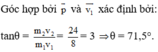
Độ lớn động lượng:
\(p=\sqrt{p_1^2+p_2^2+2p_1p_2cos60^0}\)
\(\Leftrightarrow p=\sqrt{\left(1\cdot3\right)^2+\left(2\cdot2\right)^2+2\cdot3\cdot1\cdot2\cdot2\cdot cos60^0}\)
\(\Leftrightarrow p=\sqrt{37}\left(kg\cdot\dfrac{m}{s}\right)\)