Người ta thả một miếng nhôm khối lượng 0,5kg vào 500g nước. Miếng nhôm nguội đi từ 80°C xuống 20°C. Hỏi nước nhận được một nhiệt lượng bằng bao nhiêu và nóng lên thêm bao nhiêu độ? Cho biết nhiệt dung riêng của nhôm là 880J/kg.k của nước là 4200J/kg.k
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Nước nhận được nhiệt lượng :
\(Q_{nh}=c.m.\Delta t=0,5.880.60=26400\left(J\right)\)
Áp dựng PTCBN , ta có :
Q nhôm tỏa = Q nước thu
Vậy nước nhận được nhiệt lượng = 26400 (J)
Nước nóng lên :
\(\Delta t_{nc}=Q_{nc}:m:c=26400:0,6:4200\approx10,5\left(^oC\right)\)
\(Q_{thu}=Q_{toả}=m_{Al}.c_{Al}.\left(t_{Al}-t\right)=0,5.880.\left(80-20\right)=26400\left(J\right)\\ Q_{thu}=26400\left(J\right)\\ \Leftrightarrow m_{H_2O}.c_{H_2O}.\left(t-t_{H_2O}\right)=26400\\ \Leftrightarrow 0,6.4200.\left(20-t_{H_2O}\right)=26400\\ \Leftrightarrow t_{H_2O}\approx9,524^oC\)
Vậy nước nóng lên khoảng 10,476 độ C

Nhiệt lượng nước nhận được bằng đúng nhiệt lượng do miếng đồng tỏa ra là:
Q2 = Q1 = m1.c1.(t1 - t) = 0,5.380.(80 - 20) = 11400 J
Độ tăng nhiệt độ của nước là:
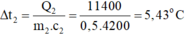

Tóm tắt:
\(m_1=0,5kg\)
\(m_2=500g=0,5kg\)
\(t_1=80^oC\)
\(t=20^oC\)
\(\Rightarrow\Delta t_1=t_1-t=80-20=60^oC\)
\(c_1=380J/kg.K\)
\(c_2=4200J/kg.K\)
===========
\(Q_2=?J\)
\(\Delta t_2=?^oC\)
Do nhiệt lượng của quả cầu tỏa ra bằng nhiệt lượng của nước nhận vào nên:
\(Q_2=Q_1=m_1.c_1.\Delta t_1=0,5.380.60=11400J\)
Nhiệt độ mà nước tăng thêm:
Theo phương trình cân bằng nhiệt:
\(Q_1=Q_2\)
\(\Leftrightarrow11400=m_2.c_2.\Delta t_2\)
\(\Leftrightarrow\Delta t_2=\dfrac{11400}{m_2.c_2}\)
\(\Leftrightarrow\Delta t_2=\dfrac{11400}{0,5.4200}\approx5,4^oC\)

Tóm tắt:
\(m_1=0,5kg\)
\(V=2l\Rightarrow m_2=2kg\)
\(t_1=75^oC\)
\(t=25^oC\)
\(\Rightarrow\Delta t_1=t_1-t=75-25=50^oC\)
\(c_1=880J/kg.K\)
\(c_2=4200J/kg.K\)
============
\(Q_2=?J\)
\(\Delta t_2=?^oC\)
Nhiệt lượng mà miếng nhôm tỏa ra:
\(Q_1=m_1.c_1.\Delta t_1=0,5.880.50=22000J\)
Do nhiệt lượng nhôm tỏa ra bằng nhiệt lượng nước thu vào:
\(Q_1=Q_2\Leftrightarrow Q_2=22000J\)
Nhiệt độ nước tăng lên thêm:
Thep phương trình cân bằng nhiệt:
\(Q_1=Q_2\)
\(\Leftrightarrow22000=m_2.c_{.2}.\Delta t_2\)
\(\Leftrightarrow\Delta t_2=\dfrac{22000}{m_2.c_2}\)
\(\Leftrightarrow\Delta t_2=\dfrac{22000}{2.4200}\approx2,6^oC\)

Ta có : Q1 = m1.c1.(t1 - t) =0.5.380.(80-20) = 11400
Q2 = m2.c2.(t - t2) = 0,5.4200.(20 - t2) = 42000 - 2100.t2
Theo pt cân bằng nhiệt , ta có :
Q1 = Q2
11400 = 42000 - 2100.t2
t2 = 14,57
t' = t - t2 = 20 - 14,57 = 5,43
Vậy nước nhận một nhiệt lượng là 11400 và nóng lên 5,43 độ
Chúc bạn học tốt ^o^

Ta có : Q1 = m1.c1.(t1 - t) =0.5.380.(80-20) = 11400
Q2 = m2.c2.(t - t2) = 0,5.4200.(20 - t2) = 42000 - 2100.t2
Theo pt cân bằng nhiệt , ta có :
Q1 = Q2
11400 = 42000 - 2100.t2
t2 = 14,57
t' = t - t2 = 20 - 14,57 = 5,43
Vậy nước nhận một nhiệt lượng là 11400 và nóng lên 5,43 độ
Chúc bạn học tốt

Ta có phương trình cân bằng nhiệt
\(Q_{thu}=Q_{toả}=0,3.880\left(100-20\right)=21120J\\\Rightarrow \Delta t^o=\dfrac{Q_{thu}}{mc}=\dfrac{21120}{0,5.4200}\approx10^o\)

Ta có phương trình cân bằng nhiệt
\(Q_{toả}=Q_{thu}\)
--> Nhiệt lượng nước nhận đc là
\(Q_{thu}=0,5.380\left(100-40\right)=11400J\)
Độ tăng nhiệt của nước
\(\Delta t=\dfrac{Q}{mc}=\dfrac{11400}{0,5.4200}=5,42^o\)

Ta có pt cân bằng nhiệt
\(Q_{thu}=Q_{tỏa}\\ \Rightarrow Q_{thu}=0,5.380\left(80-20\right)=11400J\)
Nước nóng thêm số độ
\(\Delta t^o=\dfrac{Q_{thu}}{mc}=\dfrac{11400}{0,5.4200}=5,42^o\)

Cân bằng nhiệt:
\(Q_n=Q_{nhom}=mc\left(t_1-t\right)=0,5\cdot880\cdot60=26400\left(J\right)\)
Nước nóng lên thêm:
\(Q_n=mc\Delta t=0,5\cdot4200\Delta t\)
\(\Leftrightarrow26400=2100\Delta t\)
\(\Leftrightarrow\Delta t\approx12,6^0C\)
Tóm tắt
\(m_1=0.5kg\\ m_2=500g=0,5kg\\ t_1=80^0C\\ t=20^0C\\ c_1=880J/kg.K\\ c_2=4200J/kg.K\\ \Rightarrow\Delta t_1=t_1-t=80-20=60^0C\)
______________
\(Q_2=?J\\ \Delta t_2=?^0C\)
Giải
Nhiệt lượng nước nhận được là:
\(Q_2=Q_1=m_1.c_1.\Delta t_1=0,5.880.60=26400J\)
Nhiệt độ mà nước nóng lên là:
\(Q_1=Q_2\\ \Leftrightarrow m_1.c_1.\Delta t_1=m_2.c_2.\Delta t_2\\ \Leftrightarrow0,5.880.60=0,5.4200.\Delta t_2\\ \Leftrightarrow26400=2100\Delta t_2\\ \Leftrightarrow\Delta t_2\approx12,6^0C\)