Câu 4: (1,5 điểm) Một cái ly thủy tinh hình nón, bán kính đáy bằng 2 cm và chiều cao bằng 6 cm. a) Tính thể tích cái ly (biết bề dày của ly không đáng kẻ). b) Người ta rót rượu vào lỵ, biết chiều cao của rượu trong ly bằng 3 cm. Tính thể tich rượu chứa trong ly. 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
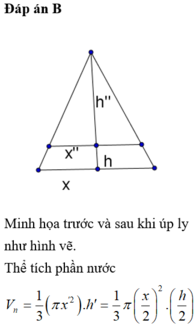
Minh họa trước và sau khi úp ly như hình vẽ.
Thể tích phần nước

Vậy chiều cao của nước và chiều cao của ly
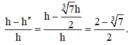

Thể tích ly 1 là:
V1=15^2*20*3,14=14130(cm3)
Thể tích ly 2 là:
V=20^2*12*3,14=15072(cm3)
Vì V1<V2 nên nước sẽ không bị tràn ra ngoài

Đáp án D
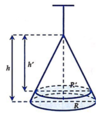
Gọi chiều cao và bán kính đường tròn đáy của chiếc ly lần lượt là h và R
Thể tích của chiếc ly V = 1 3 π R 2 h .
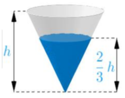
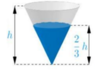
Khi để cốc theo chiều xuôi thì lượng nước trong cốc là hình nón có chiều cao và bán kính đường tròn đáy lần lượt là h 3 và R 3 .
Thể tích của lượng nước V 1 = 1 3 π R 3 2 h 3 = V 27 .
Thể tích phần không chứa nước V 2 = 26 V 27 .
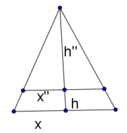
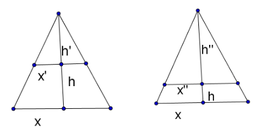
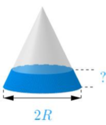
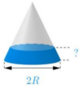
* Khi úp ngược ly lại thì phần thể tích nước trong ly không đổi và lúc đó phần không chứa nước là hình nón. Gọi h ' và R ' lần lượt là chiều cao và bán kính đường tròn đáy của phần hình nón không chứa nước. Ta có R ' R = h ' h và phần thể tích hình nón không chứa nước là
V 2 = 26 26 . V ⇔ 1 3 π R ' 2 . h ' = 26 27 . 1 3 π R 2 h ⇔ R ' 2 . h ' R 2 . h = 26 27 ⇔ h ' h 3 = 26 27 ⇔ h ' h = 26 3 3
Vậy tỷ lệ chiều cao của mực nước và chiều cao của ly nước trong trường hợp úp ngược ly là
h − h ' h = 1 − h ' h = 1 − 26 3 3 = 3 − 26 3 3

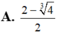
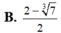
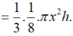

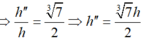
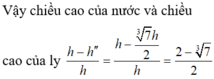


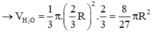
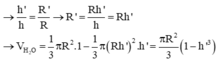



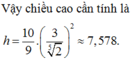

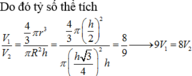



a) Thể tích cái ly:
\(V=\dfrac{1}{3}\pi r^2h=\dfrac{1}{3}\pi.2^2.6=8\pi\) \(\left(cm^3\right)\)
b) Thể tích rượu chứa trong ly:
\(V=\dfrac{1}{3}\pi r^2h_r=\dfrac{1}{3}\pi.2^2.3=4\pi\) \(\left(cm^3\right)\)
Sửa lại câu b) nhé em!
Do A'B' // AB và A' là trung điểm của OA
\(\Rightarrow A'B'\) là đường trung bình của \(\Delta OAB\)
\(\Rightarrow A'B'=\dfrac{1}{2}AB=\dfrac{1}{2}.2=1\left(cm\right)\)
Thể tích rượu trong ly:
\(V=\dfrac{1}{3}\pi r^2h_r==\dfrac{1}{3}\pi.1^2.3=\pi\left(cm^3\right)\)