Cho hàm số y = (2015 – m )x2. Xác định m để hàm số nghịch biến khi x > 0.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
13 tháng 4 2017
Khi x >0 thì hàm số nghịch biến khi 2015-m<0<=>m>2015
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 3 2023
a.
Hàm số nghịch biến khi \(x< 0\Rightarrow-3m-2>0\Rightarrow m< -\dfrac{2}{3}\)
b.
Do \(a=m^2-2m+3=\left(m-1\right)^2+2>0;\forall m\)
\(\Rightarrow\) Hàm đồng biến khi \(x>0\) và nghịch biến khi \(x< 0\)
c.
Hàm đồng biến khi \(x>0\Rightarrow2m+3>0\)
\(\Rightarrow m>-\dfrac{3}{2}\)
CM
31 tháng 7 2018
y = –( m 2 + 5m) x 3 + 6m x 2 + 6x – 5
y′ = –3( m 2 + 5m) x 2 + 12mx + 6
Hàm số đơn điệu trên R khi và chỉ khi y’ không đổi dấu.
Ta xét các trường hợp:
+)
m
2
+ 5m = 0 ⇔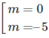 
– Với m = 0 thì y’ = 6 nên hàm số luôn đồng biến.
– Với m = -5 thì y’ = -60x + 6 đổi dấu khi x đi qua .
+) Với m 2 + 5m ≠ 0. Khi đó, y’ không đổi dấu nếu
∆ ' = 36 m 2 + 18( m 2 + 5m) ≤ 0 ⇔ 3 m 2 + 5m ≤ 0 ⇔ –5/3 ≤ m ≤ 0
– Với điều kiện đó, ta có –3( m 2 + 5m) > 0 nên y’ > 0 và do đó hàm số đồng biến trên R.
Vậy với điều kiện –5/3 ≤ m ≤ 0 thì hàm số đồng biến trên R.
CM
13 tháng 12 2017
a) y = –( m 2 + 5m) x 3 + 6m x 2 + 6x – 5
y′ = –3( m 2 + 5m) x 2 + 12mx + 6
Hàm số đơn điệu trên R khi và chỉ khi y’ không đổi dấu.
Ta xét các trường hợp:
+) m2 + 5m = 0 ⇔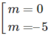 
– Với m = 0 thì y’ = 6 nên hàm số luôn đồng biến.
– Với m = -5 thì y’ = -60x + 6 đổi dấu khi x đi qua .
+) Với m 2 + 5m ≠ 0. Khi đó, y’ không đổi dấu nếu
Δ' = 36 m 2 + 18( m 2 + 5m) ≤ 0 ⇔ 3 m 2 + 5m ≤ 0 ⇔ –5/3 ≤ m ≤ 0
– Với điều kiện đó, ta có –3( m 2 + 5m) > 0 nên y’ > 0 và do đó hàm số đồng biến trên R.
Vậy với điều kiện –5/3 ≤ m ≤ 0 thì hàm số đồng biến trên R.
b) Nếu hàm số đạt cực đại tại x = 1 thì y’(1) = 0. Khi đó:
y′(1) = –3
m
2
– 3m + 6 = 0 ⇔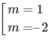 
Mặt khác, y” = –6( m 2 + 5m)x + 12m
+) Với m = 1 thì y’’ = -36x + 12. Khi đó, y’’(1) = -24 < 0 , hàm số đạt cực đại tại x = 1.
+) Với m = -2 thì y’’ = 36x – 24. Khi đó, y’’(1) = 12 > 0, hàm số đạt cực tiểu tại x = 1.
Vậy với m = 1 thì hàm số đạt cực đại tại x = 1.
16 tháng 4 2021
a) Để hàm số đạt giá trị nhỏ nhất bằng 0 khi x=0 thì 2m-1>0
\(\Leftrightarrow2m>1\)
hay \(m>\dfrac{1}{2}\)
16 tháng 4 2021
b) Để hàm số đồng biến khi x<0 và nghịch biến khi x>0 thì 2m-1<0
\(\Leftrightarrow2m< 1\)
hay \(m< \dfrac{1}{2}\)
TN
29 tháng 11 2021
Hàm số y = (m+1)x -2m là hàm bậc nhất khi m+1 ≠ 0 ⇔ m ≠ - 1
a) Hàm số nghịch biến trên R khi a < 0 ⇔ m + 1< 0 ⇔ m < - 1
kết hợp với điều kiện. Vậy m < -1
b) Khi m = 1 ta được: y = (1+1)x - 2.1 hay y = 2x - 2
Đồ thị hàm số y = 2x - 2 đi qua hai điểm A(0;-2) và B(1;0)
c) Đồ thị của hai hàm số song song với nhau khi \(\left\{{}\begin{matrix}a=a'\\b\ne b'\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m+1=3\\-2m\ne6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=2\\m\ne-3\end{matrix}\right.\)
kết hợp với điều kiện. Vậy m = 2
C
30 tháng 11 2021
Tham Khảo:
Hàm số y = (m+1)x -2m là hàm bậc nhất khi m+1 ≠ 0 ⇔ m ≠ - 1
a) Hàm số nghịch biến trên R khi a < 0 ⇔ m + 1< 0 ⇔ m < - 1
kết hợp với điều kiện. Vậy m < -1
b) Khi m = 1 ta được: y = (1+1)x - 2.1 hay y = 2x - 2
Đồ thị hàm số y = 2x - 2 đi qua hai điểm A(0;-2) và B(1;0)
c) Đồ thị của hai hàm số song song với nhau khi
kết hợp với điều kiện. Vậy m = 2
Để hàm số nghịch biến khi x>0 thì 2015-m<0
=>m>2015