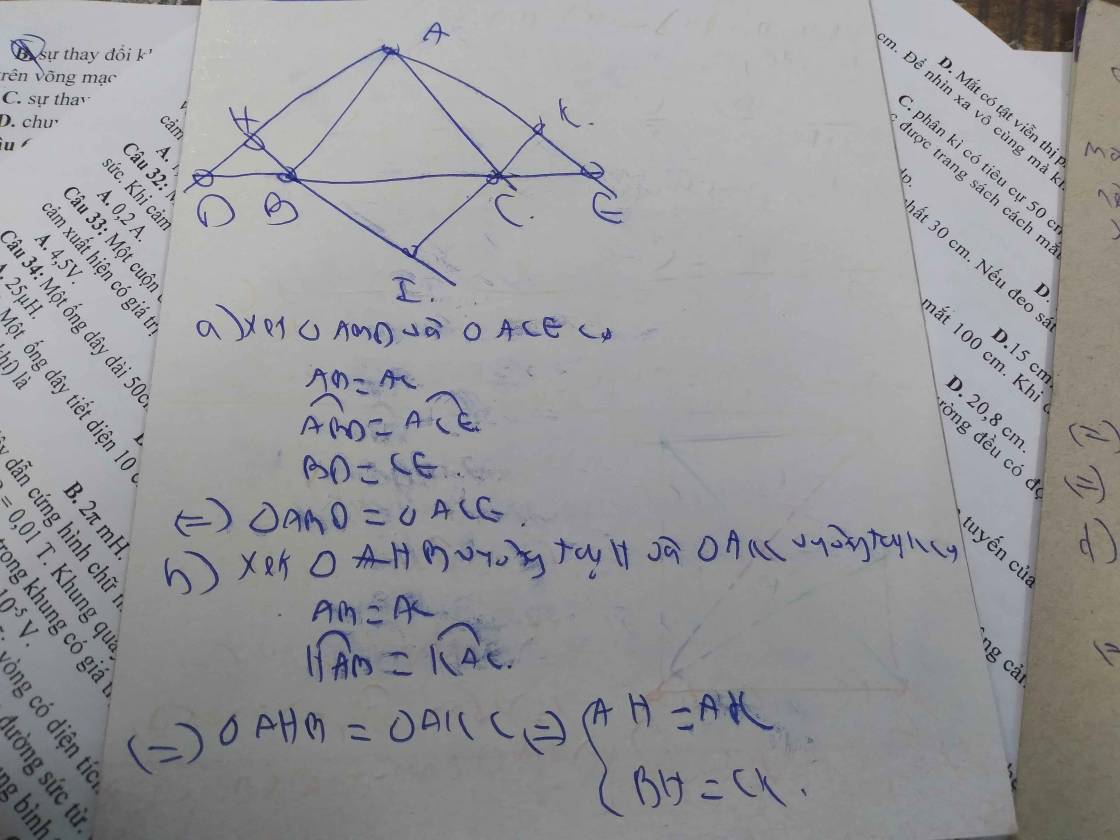
Cho tam giác ABC cân trên tia đối tia BC lấy D trên tia đối CB lấy E sao cho BD=CE
a)tam giác ABD=tam giác ACE
b)vẽ BH vuông góc AD vễ CK vuông góc AE cm BH=CK
c) Tia HB cắt KC tại I cm AI là phân giác BAC
d)HK sonh song DE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
22 tháng 4 2023
Đúng(1)
Những câu hỏi liên quan
3 tháng 2 2021
a) Ta có: \(\widehat{ABD}+\widehat{ABC}=180^0\)(hai góc kề bù)
\(\widehat{ACE}+\widehat{ACB}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔABC cân tại A)
nên \(\widehat{ABD}=\widehat{ACE}\)
Xét ΔABD và ΔACE có
AB=AC(ΔABC cân tại A)
\(\widehat{ABD}=\widehat{ACE}\)(cmt)
BD=CE(gt)
Do đó: ΔABD=ΔACE(c-g-c)
b) Ta có: ΔABD=ΔACE(cmt)
nên AD=AE(hai cạnh tương ứng)
Xét ΔADE có AD=AE(cmt)
nên ΔADE cân tại A(Định nghĩa tam giác cân)
c) Xét ΔDHB vuông tại H và ΔEKC vuông tại K có
DB=CE(gt)
\(\widehat{HDB}=\widehat{KEC}\)(hai góc ở đáy của ΔADE cân tại A)
Do đó: ΔDHB=ΔEKC(cạnh huyền-góc nhọn)
d) Ta có: ΔDHB=ΔEKC(cmt)
nên \(\widehat{HBD}=\widehat{KCE}\)(hai góc tương ứng)
mà \(\widehat{HBD}=\widehat{OBC}\)(hai góc đối đỉnh)
và \(\widehat{KCE}=\widehat{OCB}\)(hai góc đối đỉnh)
nên \(\widehat{OBC}=\widehat{OCB}\)
Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)(cmt)
nên ΔOBC cân tại O(Định lí đảo của tam giác cân)
e) Xét ΔABO và ΔACO có
AB=AC(ΔABC cân tại A)
AO chung
BO=CO(ΔOBC cân tại O)
Do đó: ΔABO=ΔACO(c-c-c)
nên \(\widehat{BOA}=\widehat{COA}\)(hai góc tương ứng)
mà tia OA nằm giữa hai tia OB,OC
nên OA là tia phân giác của \(\widehat{BOC}\)(đpcm)
7 tháng 1
Ta có: \(\widehat{ABD}+\widehat{ABC}=180^0\)(hai góc kề bù)
\(\widehat{ACE}+\widehat{ACB}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{ABD}=\widehat{ACE}\)
Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
=>AD=AE và \(\widehat{ADB}=\widehat{AEC}\)
Xét ΔHBD vuông tại H và ΔKCE vuông tại K có
BD=CE
\(\widehat{HDB}=\widehat{KEC}\)
Do đó; ΔHBD=ΔKCE
=>\(\widehat{HBD}=\widehat{KCE}\)
mà \(\widehat{HBD}=\widehat{OBC}\)(hai góc đối đỉnh)
và \(\widehat{KCE}=\widehat{OCB}\)(hai góc đối đỉnh)
nên \(\widehat{OBC}=\widehat{OCB}\)
=>OB=OC
Xét ΔABO và ΔACO có
AB=AC
BO=CO
AO chung
Do đó: ΔABO=ΔACO
=>\(\widehat{BOA}=\widehat{COA}\)
=>OA là phân giác của góc BOC
23 tháng 2 2022
a: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó:ΔABM=ΔACN
b: Xét ΔHMB vuông tại H và ΔKNC vuông tại K có
MB=NC
\(\widehat{M}=\widehat{N}\)
Do đó: ΔHMB=ΔKNC
Suy ra: BH=CK
c: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
BH=CK
Do đó:ΔABH=ΔACK
Suy ra: AH=AK
Xét ΔAMN có AH/AM=AK/AN
nên HK//MN
hay HK//BC
d: Ta có: ΔHBM=ΔKCN
nên \(\widehat{HBM}=\widehat{KCN}\)
=>\(\widehat{OBC}=\widehat{OCB}\)
hay ΔOBC cân tại O
22 tháng 4 2023
a: Xet ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔABD=ΔACE
=>AD=AE
b: ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông góc BC
ΔADE cân tại A
mà AM là đường cao
nên AM là phân giác của góc DAE
c: Xet ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc HAB=góc KAC
=>ΔAHB=ΔAKC
d: Xét ΔAED có
AH/AD=AK/AE
nên HK//DE
23 tháng 4 2023
a: Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔABD=ΔACE
=>AD=AE
b: ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông góc BC
ΔADE cân tại A
mà AM là đường cao
nên AM là phân giác của góc DAE
c: Xet ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH=góc CAK
=>ΔAHB=ΔAKC
d: Xét ΔADE có AH/AD=AK/AE
nên HK//DE
3 tháng 2 2021
a, Xét tam giác abd và tam giác ace có
ab=ac(tam giác abc cân tại a)
bd=ce(theo cách vẻ hình)
góc abd = góc ace
31 tháng 1 2022
a) Xét \(\Delta ADB\) và \(\Delta AEC\) có:
\(AB=AC\) (do \(\Delta ABC\) cân tại \(A\))
\(\widehat{ABD}=\widehat{ACE}\)
\(BD=CE\) (giả thiết)
\(\Rightarrow\Delta ADB=\Delta AEC\left(c.g.c\right)\)
\(\Rightarrow AD=AE\) (\(2\) cạnh tương ứng)
\(\Rightarrow\Delta ADE\) cân tại \(A\)
b) Vì \(\Delta ADE\) cân tại \(A\)
\(\Rightarrow\widehat{ADB}=\widehat{ACE}\) (\(2\) góc tương ứng)
Ta có: \(\left\{{}\begin{matrix}\widehat{ADB}+\widehat{HBD}=90^o\\\widehat{ACE}+\widehat{KCE}=90^o\end{matrix}\right.\) (\(2\) góc phụ nhau)
Từ hai điều trên \(\Rightarrow\widehat{HBD}=\widehat{KCE}\)
Mà \(\left\{{}\begin{matrix}\widehat{HBD}=\widehat{CBI}\\\widehat{KCE}=\widehat{BCI}\end{matrix}\right.\) (\(2\) góc đối đỉnh)
Từ đó \(\Rightarrow\widehat{CBI}=\widehat{BCI}\)
\(\Rightarrow\Delta BIC\) cân tại \(I\)
c) Xét \(\Delta ABI\) và \(\Delta ACI\) có:
\(AB=AC\) (giả thiết)
\(BI=CI\) (do \(\Delta BIC\) cân tại \(I\))
\(AI\) là cạnh chung
\(\Rightarrow\Delta ABI=\Delta ACI\left(c.c.c\right)\)
\(\Rightarrow\widehat{AIB}=\widehat{AIC}\) (\(2\) góc tương ứng)
\(\Rightarrow AI\) là tia phân giác \(\widehat{BIC}\)
14 tháng 2 2022
a; Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
Suy ra: AD=AE
hay ΔADE cân tại A
b: Xét ΔHBD vuông tại H và ΔKCE vuông tại K có
BD=CE
\(\widehat{D}=\widehat{E}\)
Do đó: ΔHBD=ΔKCE
Suy ra: \(\widehat{HBD}=\widehat{KCE}\)
hay \(\widehat{IBC}=\widehat{ICB}\)
hay ΔIBC cân tại I