Cho tam giác ABC có góc A=90 độ , đường cao AH. Gọi D, E theo thứ tự là trung điểm của HB và AH.
Chứng minh rằng : CE vuông góc với AD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 5 2022
a, Xét Δ ABC, có :
\(AB^2+AC^2=BC^2\) (định lí Py - ta - go)
=> \(3^2+4^2=BC^2\)
=> \(25=BC^2\)
=> BC = 5 (cm)
Xét Δ ABC vuông tại A, theo hệ thức lượng có :
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
=> \(\dfrac{1}{AH^2}=\dfrac{1}{3^2}+\dfrac{1}{4^2}\)
=> AH = 2,4 cm
b, Xét Δ ABD, có :
HD = HB (gt)
AH là đường cao
=> Δ ABD cân
2 tháng 9 2021
a: Xét tứ giác ADHE có
\(\widehat{EAD}=\widehat{AEH}=\widehat{ADH}=90^0\)
Do đó: ADHE là hình chữ nhật
Suy ra: AH=DE
TB
18 tháng 11 2021
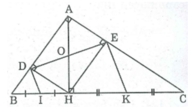
Tam giác BDH vuông tại D có DI là đường trung tuyến thuộc cạnh huyền BH
⇒ DI = IB = 1/2 BH (tính chất tam giác vuông)
⇒ ∆ IDB cân tại I ⇒ ∠ (DIB) = 180 0 - 2. ∠ B (1)
Tam giác HEC vuông tại E có EK là đường trung tuyến thuộc cạnh huyền HC.
⇒ EK = KH = 1/2 HC (tính chất tam giác vuông) .
⇒ ∆ KHE cân tại K ⇒ ∠ (EKH) = 180 0 - 2. ∠ (KHE) (2)
Tứ giác ADHE là hình chữ nhật nên:
HE // AD hay HE // AB ⇒ ∠ B = ∠ (KHE) (đồng vị)
Từ (1), (2) và (3) suy ra: ∠ (DIB) = ∠ (EKH)
Vậy DI // EK (vì có cặp góc đồng vị bằng nhau).
CM
26 tháng 12 2017
Tam giác BDH vuông tại D có DI là đường trung tuyến thuộc cạnh huyền BH
⇒ DI = IB = 1/2 BH (tính chất tam giác vuông)
⇒ ∆ IDB cân tại I ⇒ ∠ (DIB) = 180 0 - 2. ∠ B (1)
Tam giác HEC vuông tại E có EK là đường trung tuyến thuộc cạnh huyền HC.
⇒ EK = KH = 1/2 HC (tính chất tam giác vuông) .
⇒ ∆ KHE cân tại K ⇒ ∠ (EKH) = 180 0 - 2. ∠ (KHE) (2)
Tứ giác ADHE là hình chữ nhật nên:
HE // AD hay HE // AB ⇒ ∠ B = ∠ (KHE) (đồng vị)
Từ (1), (2) và (3) suy ra: ∠ (DIB) = ∠ (EKH)
Vậy DI // EK (vì có cặp góc đồng vị bằng nhau).
26 tháng 4 2020
cho tam giác ABC và 3 điểm A',B',C' lần lượt nằm trên 3 cạnh BC,AC,AB ( A',B',C' không trùng với các đỉnh của tam giác )
Khi đó ta có : AA',BB',CC' đồng quy \(\Leftrightarrow\frac{A'B}{A'C}.\frac{B'C}{B'A}.\frac{C'A}{C'B}=1\)
26 tháng 4 2020
Gọi P là giao điểm của AD và BE
Áp dụng định lí Ceva vào \(\Delta ABE\),ta có :
\(\frac{BP}{PE}.\frac{HE}{AH}.\frac{AM}{BM}=1\Rightarrow\frac{AH}{HE}=\frac{BP}{PE}\Rightarrow PH//AB\)
\(\Rightarrow\widehat{BAD}=\widehat{DPH}\)
Mà \(\widehat{BAD}=\widehat{DAH}\)
\(\Rightarrow\widehat{DAH}=\widehat{PDH}\Rightarrow\Delta AHP\)cân tại H
\(\Rightarrow HP=AH\)
Cần chứng minh \(DP//CE\Leftrightarrow\frac{BD}{BC}=\frac{BP}{BE}\Leftrightarrow\frac{BD}{BC}=1-\frac{EP}{BE}\)
Ta có : \(\frac{EP}{BE}=\frac{HP}{AB}=\frac{AH}{AB}=\frac{HD}{BD}\)
Khi đó : \(\frac{BD}{BC}=1-\frac{HD}{BD}\Leftrightarrow\frac{BD}{BC}+\frac{HD}{BD}=1\Leftrightarrow BD^2+HD.BC=BC.BD=\left(BD+DC\right).BD\)
\(\Rightarrow HD.BC=CD.BD\Rightarrow\frac{HD}{BD}=\frac{CD}{BC}\Leftrightarrow\frac{AH}{AB}=\frac{CD}{BC}\)
Ta có : \(\widehat{CDA}=\widehat{DBA}+\widehat{BAD}=\widehat{CAH}+\widehat{DAH}=\widehat{CAD}\)
\(\Rightarrow\Delta CAD\)cân tại C \(\Rightarrow CD=CA\)
Từ đó suy ra : \(\frac{AH}{AB}=\frac{AC}{BC}\) ( đúng vì \(\Delta AHB~\Delta CAB\left(g.g\right)\))
Vậy ta có đpcm
C
15 tháng 8 2023
Xét tứ giác AEHD, có:
∠A = ∠E = ∠D = 90°
=> tứ giác AEHD là hình chữ nhật.
O là giao điểm hai đường chéo hcn AEHD
=> OD = OH (1).
DI là đường trung tuyến ứng với cạnh huyền của Δ vuông DHB
=> DI = 1/2 BH = IH (2).
Xét Δ IDO và Δ IHO, có:
OD = OH (1).
OI là cạnh chung.
DI = IH (2).
=> Δ IDO = Δ IHO (đpcm).
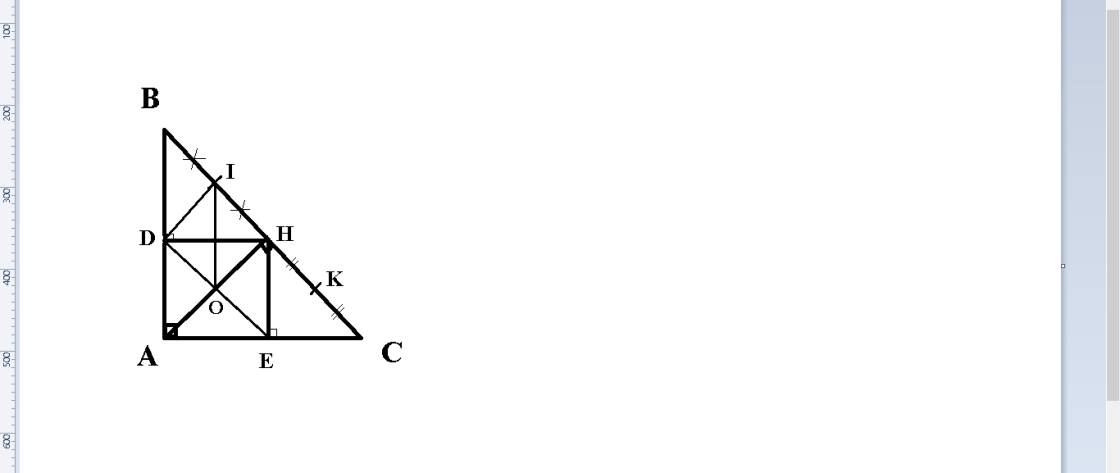
(bồ xem thử ổn hông nhe).
TH
11 tháng 12 2021
cho tam giác ABC vuông tại A đường cao AH ( H thuộc cạnh BC) .gọi D, E theo thứ tự chân đường vuông góc kẻ từ H đến AB và AC .Gọi M, N theo thứ tự là trung điểm của BH và CH .Gọi I là giao điểm của AH và ED
1: cm tam giác DHE là tam giác vuông.Biết AB=3,AC=4, tính
a: bán kính của đường tròn ngoại tiếp tam giác DHE
b: cos ACH
2: cm ED là tiếp tuyến của đường tròn đg kính CH
3: cm I thuộc đg tròn đg kính Mn
ảo à
đéo chứng minh được nhé
tự vẽ hình kiểm chứng đi
t.i.c.k mik mik t.i.c.k lại