cho hai góc kề bù \(\widehat{xOz}\) và \(\widehat{zOy}\), \(\widehat{xOz}\)= 62 độ, và Ot là tia phân giác của góc \(\widehat{zoy}\). Tính \(\widehat{tOy}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 9 2023
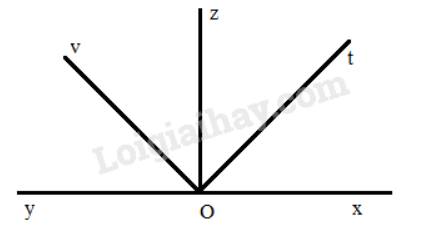
Vì Oz là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy}\) = \(\frac{1}{2}.180^\circ = 90^\circ \)
Vì Ot là tia phân giác của \(\widehat {xOz}\) nên \(\widehat {xOt} = \widehat {tOz} = \frac{1}{2}\widehat {xOz} = \frac{1}{2}.90^\circ = 45^\circ \)
Vì Ov là tia phân giác của \(\widehat {zOy}\) nên \(\widehat {yOv} = \widehat {vOz} = \frac{1}{2}\widehat {zOy} = \frac{1}{2}.90^\circ = 45^\circ \)
Mà tia Oz nằm trong \(\widehat {tOv}\) nên \(\widehat {tOv}= \widehat {tOz} + \widehat {zOv} = 45^\circ + 45^\circ = 90^\circ \)
Vậy \(\widehat {tOv} = 90^\circ \)
19 tháng 9 2023
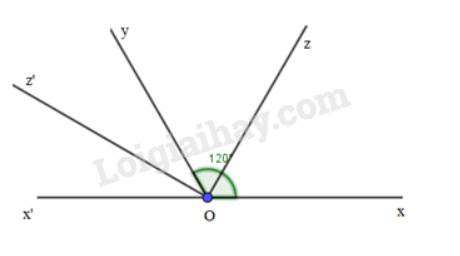
Vì Oz là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.120^\circ = 60^\circ \)
Vì Oz’ là tia phân giác của \(\widehat {yOx'}\) nên \(\widehat {x'Oz'} = \widehat {yOz'} = \frac{1}{2}.\widehat {yOx'} = \frac{1}{2}.60^\circ = 30^\circ \)
Vì tia Oy nằm trong \(\widehat {zOz'}\) nên \(\widehat {zOz'}=\widehat {zOy} + \widehat {yOz'} = 60^\circ + 30^\circ = 90^\circ \)
Vậy \(\widehat {zOy} = 60^\circ ,\widehat {yOz'} = 30^\circ ,\widehat {zOz'} = 90^\circ \)
Chú ý:
2 tia phân giác của 2 góc kề bù thì vuông góc với nhau
24 tháng 3 2020
Bài làm
Bài 1:
a) Trên nửa mặt phẳng có bờ chứa tia Ox có:
OB > OM ( 4 cm > 1 cm )
=> M nằm giữa hai điểm B và O
Ta có: OM + BM = OB
Hay 1 + BM = 4
=> BM = 4 - 1 = 3
Lại có: MO + OA = MA
Hay 1 + 2 = MA
=> MA = 3
Mà BM = 3
=> MA = BM ( 3cm = 3cm )
=> M là trung điểm của AB.
b) Trên nửa mặt phẳng có bờ chứa tia Oy có:
^zOy < ^tOy ( 30° < 130° )
=> Oz nằm giữa hai tia Ot và Oy.
Ta có: ^tOz + ^zOy = ^tOy
Hay ^tOz + 30° = 130°
=> ^tOz = 130° - 30° = 100°
H
7 tháng 3 2018
a, Ta có : \(\widehat{yOz}=\widehat{xOz}-\widehat{xOy}=100^o-30^o=70^o\)
b, Vì Ot là phân giác góc xOz nên :
\(\widehat{zOt}=\frac{1}{2}\widehat{xOz}=50^o\)
=> \(\widehat{yOt}=\widehat{yOz}-\widehat{zOt}=70^o-50^o=20^o\)
c, Các cặp góc kề bù : yOt và tOy' ; yOz và y'Oz ; xOy và xOy' .
YN
23 tháng 2 2022
`Answer:`
Ta có `hat{zOt}+\hat{yOz}=90^o`
\(\Rightarrow\frac{1}{2}.Oz+\widehat{yOz}=90^o\)
\(\Rightarrow\frac{1}{2}.4\widehat{yOz}+\widehat{yOz}=90^o\)
\(\Rightarrow\widehat{yOz}.3=90^o\)
\(\Rightarrow\widehat{yOz}=30^o\)
`=>\hat{xOz}=120^o` (Vì `\hat{xOz}=4\hat{yOz}`
Vậy `\hat{xOy}=\hat{yOz}+\hat{xOz}=120^o+30^o=150^o`
(Bạn tự vẽ hình nhé!)
Ta có: góc xOz + góc zOy = 180 độ (kề bù)
=> 62 + góc zOy = 180
=> góc zOy = 180 - 62 = 118 độ
Vì Ot là phân giác góc zOy => góc tOy = góc tOz = góc zOy : 2 = 118 : 2 = 59 độ
toy=59 do
ket ban voi minh