Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
A/
* Xét T/g AOM và T/g BOM có :
+ O1 = O2 ( Oz là p/g AOB )
+ OAM = OBM ( = 900 )
+ AM chung
=> t/g AOM = BOM ( ch.gn )
* Xét T/g AMH và T/g BMH có :
+ AM = BM ( T/g AOM= BOM )
+ Góc AMH = BMH ( T/g AOM = BOM )
+ MH chung
=> T/g AMH = T/g BMH (c.g.c)
=> AH = BH
* Xét t/g AOH và T/g BOH có :
+ AH = BH ( cmt )
+ OH chung
+ OA = OB ( T/g AOM = T/g BOM )
=> T/g AOH = T/g BOH (c.c.c)
* Ta có :
+ AH = BH ( cmt ) (1)
+ H1 = H2 ( T/g AOH = T/g BOH ) (2)
mà H1 + H2 = 180o ( Kb )
- (1) , (2) => H1 = H2 = 90o
=> OM là trung trực của đoạn thẳng AB
B/ Xét T/g AMD và T/g BMC có :
+ AM = BM ( T?g AOM = T/g BOM )
+ Góc DAM = CAM ( = 90o )
+ M1 = M2 ( đđ )
=> T/g AMD = T/g BMC ( ch. gn )
=> MD = MC
=> T/g DMC cân tại D
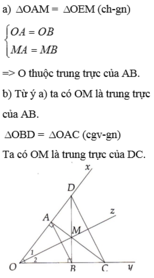
a) Xét ΔAOM và ΔBOM có:
+ Góc AOM = BOM.
+ OM là cạnh huyền chung.
+ Góc OAM = OBM = 90.
Nên ΔAOM = ΔBOM (ch-gn).
=>OM là đường trung trực của đoạn thẳng AB.
b) tam giác DMC là tam giác cân.
Xét ΔADM và ΔBCM có:
+ Góc MAD = MBC = 90.
+ Góc AMD = CMB (đối đỉnh).
+ AM = BM (ΔAOM = ΔBOM).
Nên ΔADM = ΔBCM (g.c.g).
=> DM = CM.
Nên ΔDMC là tam giác cân.
c) Ta có ΔDMC là tam giác cân, Nên DM + MC > DC.
Xét ΔADM có AM là cgv nên: AM< DM =>2AM < DC.
<=> AM + DM < DC