Cho hình vuông ABCD, trên tia đối của tia BA lấy điểm E. Đường thẳng EC cắt đường thẳng AD tại F. Gọi H là giao điểm của BC và ED, G là giao điểm của FB và CD.
1. Tính giá trị biểu thức AC/FA + AC/EA
2. Gọi giao điểm của AC và BF là O. Chứng minh rằng EO đi qua trung điểm của đoạn thẳng AF.

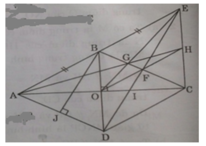
Các bạn giúp mình ý 2 với ạ
GỢI Ý
Bạn tự vẽ hình.
1) Gọi độ dài cạnh của hình vuông ABCD là a (\(AB=BC=CD=DA=a\))
△DCF∼△BEC (g-g) \(\Rightarrow\dfrac{DF}{a}=\dfrac{a}{BE}\)
BE//CD \(\Rightarrow\dfrac{a}{BE}=\dfrac{CH}{BH}\)
DF//BC \(\Rightarrow\dfrac{DF}{a}=\dfrac{DG}{CG}\)
\(\Rightarrow\dfrac{DG}{CG}=\dfrac{CH}{BH}\Rightarrow\dfrac{DG}{CH}=\dfrac{CG}{BH}=\dfrac{DG+CG}{CH+BH}=\dfrac{DC}{BC}=1\)
\(\Rightarrow DG=CH;CG=BH\)
△ADE∼△CHD \(\Rightarrow\dfrac{a}{AE}=\dfrac{CH}{a}\left(1\right)\)
△BCG∼△FAB \(\Rightarrow\dfrac{a}{AF}=\dfrac{CG}{a}\left(2\right)\)
\(\left(1\right)+\left(2\right)\Rightarrow a\left(\dfrac{1}{AE}+\dfrac{1}{AF}\right)=\dfrac{CH+CG}{a}=\dfrac{CH+BH}{a}=1\)
\(\Rightarrow\dfrac{AC}{AE}+\dfrac{AC}{AF}=\sqrt{2}\)
b) BỔ ĐỀ HÌNH THANG: Trong hình thang, đường thẳng tạo bởi giao điểm của hai đường chéo và giao điểm của hai cạnh bên thì đi qua 2 trung điểm của hai đáy.
Quay lại bài toán:
Qua O kẻ đường thẳng // với AF cắt AB, CF tại X,Y.
*Chứng minh OX=OY (dùng định lí Thales giới hạn trong các tam giác trong hình thang ABCF).
*Chứng minh K là trung điểm AF (dùng định lí Thales trong các tam giác AKE, FKE).