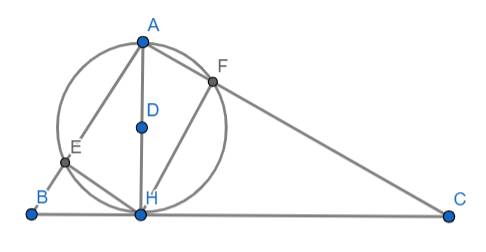
Bài 1. Cho tam giác ABC vuông tại A (AB < AC) có đường cao AH. Đường tròn (K).đường kính AH cắt các cạnh AB, AC tại E, F khác A. Gọi M, N là trung điểm các cạnh HB, HC
a) chứng minh: Tứ giác AEHF là hình chữ nhậtb) Chứng minh hai tam giác AEF, ACB đồng dạng và tứ giác BCFE nội tiếp.c) Chứng minh ME, NF là tiếp tuyến của (K).
.

a: góc AEH=góc AFH=góc FAE=90 độ
=>AEHF là hình chữ nhật
b: ΔAHB vuông tại H có HE là đường cao
nên AE*AB=AH^2
ΔAHC vuông tại H có HF là đường cao
nên AF*AC=AH^2=AE*AB
=>AE/AC=AF/AB
=>ΔAEF đồng dạng vơi ΔACB