Một vật đặt trước thấu kính cho ảnh cùng chiều và lớn hơn gấp 3 lần vật. Biết khoảng cách giữa ảnh và vật là 20 cm.
a. Thấu kính sử dụng loại gì
b. Xác định vị trí vật, vị trí ảnh và tiêu cự thấu kính
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Do hứng được ảnh trên màn nên thấu kính đã sử dụng là thấu kính hội tụ.
b)
Đổi : \(AB=h=5\left(mm\right)=0,5\left(cm\right)\)
Xét \(\Delta OAB\sim\Delta OA'B'\) : \(\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}\) (*)
Xét \(\Delta F'OI\sim\Delta F'A'B'\) : \(\dfrac{OI}{A'B'}=\dfrac{OF'}{F'A'}\).
Mà \(OI=AB\) và \(F'A'=OA'-OF'\) nên \(\dfrac{AB}{A'B'}=\dfrac{OF'}{OA'-OF'}\).
Từ đó, suy ra : \(\dfrac{OA}{OA'}=\dfrac{OF'}{OA'-OF'}\Leftrightarrow\dfrac{18}{d'}=\dfrac{12}{d'-12}\Leftrightarrow d'=36\left(cm\right)\)
Thay lại vào (*) ta được : \(\dfrac{18}{36}=\dfrac{0,5}{h'}\Leftrightarrow h'=1\left(cm\right)\)
Vậy : Ảnh ở vị trí cách thấu kính 36cm và cao 1cm.

a)Độ tụ của thấu kính:
\(D=\dfrac{1}{f}=\dfrac{1}{20}\)
b)\(d=60cm\Rightarrow\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow d'=30cm\)
\(\Rightarrow\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow h'=1cm\)
Các trường hợp sau tương tự nhé.

Đáp án: A
Vật thật cho ảnh cùng chiều, nhỏ hơn vật 2 lần nên ảnh là ảnh ảo và d’ = -6cm.
Theo công thức thấu kính và công thức số phóng đại:
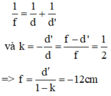
Đây là thấu kính phân kỳ.
Vị trí của vật để có ảnh nhỏ hơn vật 3 lần là d 2 , khi đó ta có:


Đáp án A
Vật thật cho ảnh cùng chiều, nhỏ hơn vật 2 lần nên ảnh là ảnh ảo và d’ = -6cm.
Theo công thức thấu kính và công thức số phóng đại:
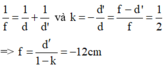
Đây là thấu kính phân kỳ.
Vị trí của vật để có ảnh nhỏ hơn vật 3 lần là d2, khi đó ta có:


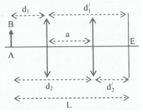
+ Theo tính thuận nghịch của chiều truyền ánh sáng 
@ Ta có thể giải cách khác như sau:
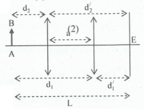

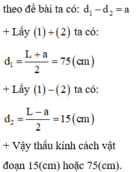

Khoảng cách giữa ảnh và vật qua thấu kính:
\(L=\left|d+d'\right|=25\Rightarrow\left[{}\begin{matrix}d+d'=25\\d+d'=-25\end{matrix}\right.\)
TH1:\(d+d'=25\Rightarrow d'=25-d\)
Vị trí ảnh: \(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{6}=\dfrac{1}{d}+\dfrac{1}{25-d}\Rightarrow d=10cm\)
\(\Rightarrow d'=25-10=15cm\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}d=10cm\\d'=15cm\end{matrix}\right.\\\left\{{}\begin{matrix}d=15cm\\d'=10cm\end{matrix}\right.\end{matrix}\right.\)
TH2:\(d+d'=-25\Rightarrow d'=-25-d\)
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{6}=\dfrac{1}{d}+\dfrac{1}{-25-d}\Rightarrow d=5cm\)
\(\Rightarrow d'=-25-5=-30cm\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}d=5cm\\d'=-30cm\end{matrix}\right.\\\left\{{}\begin{matrix}d=-30cm\\d'=5cm\end{matrix}\right.\end{matrix}\right.\)
Vậy số trường hợp xảy ra là:
\(\left[{}\begin{matrix}TH1\\\left\{{}\begin{matrix}d=5cm\\d'=-30cm\end{matrix}\right.\end{matrix}\right.\)

Sơ đồ tạo ảnh:
![]()
Khoảng cách giữa vật và ảnh qua thấu kính L = |d + d'|
Vì ảnh thật qua thấu kính hội tụ cho ảnh cùng chiều vật nên ảnh này là ảnh ảo, mà ảnh ảo của vật thật qua thấu kính hội tụ cao hơn vật nên:

Từ (1) và (2) ta có hệ phương trình:
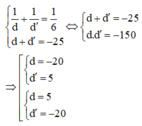
Vì vật là vật thật, ảnh ảo nên ta có 1 nghiệm thỏa mãn bài toán:
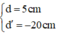
a. Vì qua thấu kính ta thu được ảnh cùng chiều và lớn hơn vật nên thấu kính đang sử dụng là thấu kính hội tụ.
b. Vì qua thấu kính hội tụ ta thu được ảnh cùng chiều và lớn hơn vật nên ảnh đó là ảnh ảo hay ảnh nằm cùng phía với vật so với thấu kính.
Ta có: \(\dfrac{h'}{h}=\dfrac{d'}{d}\Leftrightarrow3=\dfrac{d'}{d'-20}\Rightarrow d'=30\left(cm\right)\) \(\Rightarrow d=d'-20=30-20=10\left(cm\right)\)
Vì ảnh thu được là ảnh ảo nên ta có công thức thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}-\dfrac{1}{d'}=\dfrac{1}{10}-\dfrac{1}{30}=\dfrac{1}{15}\Rightarrow f=15\left(cm\right)\)
Vậy vị trí của vật cách thấu kính một khoảng 10cm, ảnh vật cách thấu kính 30cm và tiêu cự thấu kính là 15cm.