Với giá trị nào của m thì f(x)=2x^2+3x-(m-1) luôn dương với mọi x thuộc R?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

23 tháng 3 2023
\(\Delta=\left(-2m+4\right)^2-4\cdot\left(-1\right)\left(m+3\right)\)
=4m^2-16m+16+4(m+3)
=4m^2-16m+16+4m+12
=4m^2-12m+28
Để f(x)<0 với mọi x thì 4m^2-12m+28<0 và -1<0
=>\(m\in\varnothing\)
LC
2

AH
Akai Haruma
Giáo viên
2 tháng 3 2021
Lời giải:
Sửa $f(x)=mx+m-2x=x(m-2)+m$
Với $m=2$ thì $f(x)=2>0$ với mọi $x$, tức là không có giá trị thực nào của $x$ để $f(x)$ âm (thỏa mãn)
Với $m\neq 2$ thì đồ thị $f(x)=x(m-2)+m$ là 1 đường thẳng tiếp tuyến, luôn tồn tại giá trị của $x$ để $f(x)$ âm.
Vậy $m=2$

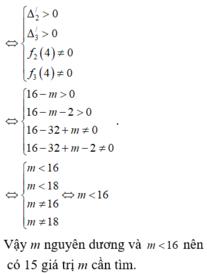

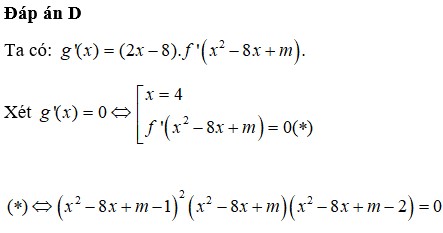
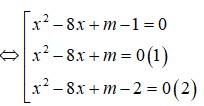

\(2x^2+3x-\left(m-1\right)>0;\forall x\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=2>0\\\Delta=9+8\left(m-1\right)< 0\end{matrix}\right.\)
\(\Rightarrow m< -\dfrac{1}{8}\)