giup em câu 1,2 luôn ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


3: \(\left(3x+5\right)\left(2x-7\right)\)
\(=6x^2-21x+10x-35\)
\(=6x^2-11x-35\)
4: \(\left(5x-2\right)\left(3x+4\right)\)
\(=15x^2+20x-6x-8\)
\(=15x^2+14x-8\)


câu 1:
gọi hóa trị của các nguyên tố cần tìm là \(x\)
\(\rightarrow H^I_1Br^x_1\rightarrow I.1=x.1\rightarrow x=I\)
vậy \(Br\) hóa trị \(I\)
\(\rightarrow H_2^IS_1^x\rightarrow I.2=x.1\rightarrow x=II\)
vậy \(S\) hóa trị \(II\)
\(\rightarrow Na_2^xO^{II}_1\rightarrow x.2=II.1\rightarrow x=I\)
vậy \(Na\) hóa trị \(I\)
các ý còn lại làm giống nhé!
câu 2:
gọi hóa trị của \(Fe\) và \(Al\) trong các hợp chất là \(x\)
\(\rightarrow Fe^x_1O^{II}_1\rightarrow x.1=II.1\rightarrow x=II\)
vậy \(Fe\) hóa trị \(II\)
\(\rightarrow Al_2^x\left(SO_4\right)_3^{II}\rightarrow x.2=II.3\rightarrow x=III\)
vậy \(Al\) hóa trị \(III\)
mấy ý còn lại làm tương tự

1.
Do $a>1$ nên $a-1>0; 2a+1>0$. Khi đó
$A=\sqrt{(a-1)^2(2a+1)^2}=\sqrt{(a-1)^2}.\sqrt{(2a+1)^2}$
$=|a-1|.|2a+1|=(a-1)(2a+1)$
2.
$B=\sqrt{(b-1)(b+7)+16}=\sqrt{b^2+6b-7+16}=\sqrt{b^2+6b+9}$
$=\sqrt{(b+3)^2}=|b+3|=-(b+3)$ do $b+3<0$ với mọi $b< -3$

Câu 2
Đổi : 72 km/h =20 m/s
Gia tốc của ô tô là
\(a=\dfrac{v^2-v_0^2}{2s}=\dfrac{20^2-4^2}{2\cdot400}=0,48\left(\dfrac{m}{s^2}\right)\)
Câu 3:
\(\dfrac{F_1}{F_2}=\dfrac{d_2}{d_1}\Rightarrow d_2=\dfrac{F_1\cdot d_1}{F_2}=\dfrac{30\cdot6}{40}=4,5\left(cm\right)\)
Khoảng cách giữa lực F1 và F2
\(d=d_1+d_2=6+4,5=10,5\left(cm\right)\)

\(1,\\ x+2\ge0\Leftrightarrow x\ge-2\)
\(\Leftrightarrow A=\)\([-2;+\infty)\)
\(5-x\ge0\Leftrightarrow x\le5\)
\(\Leftrightarrow B=\)\((-\infty;5]\)
\(\Leftrightarrow A\cap B=\left[-2;5\right]\)
\(2,A\cup B=\varnothing\)

1.
Phương trình có 2 nghiệm dương pb khi:
\(\left\{{}\begin{matrix}\Delta'=\left(m+1\right)^2-\left(2m+46\right)=m^2-45>0\\x_1+x_2=2\left(m+1\right)>0\\x_1x_2=2m+46>0\end{matrix}\right.\) \(\Rightarrow m>3\sqrt{5}\)
Khi đó:
\(\left|\sqrt{x_1}-\sqrt{x_2}\right|=2\)
\(\Leftrightarrow x_1+x_2-2\sqrt{x_1x_2}=4\)
\(\Leftrightarrow2\left(m+1\right)-2\sqrt{2m+46}=4\)
\(\Leftrightarrow2m+46-2\sqrt{2m+46}-48=0\)
Đặt \(\sqrt{2m+46}=a>0\)
\(\Rightarrow a^2-2a-48=0\Leftrightarrow\left[{}\begin{matrix}a=8\\a=-6\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{2m+46}=8\)
\(\Rightarrow m=9\)
2.
Kết hợp pt thứ 2 và điều kiện đề bài ta được:
\(\left\{{}\begin{matrix}mx+3y=m+3\\x-3y=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\left(m+1\right)x=m+5\\x-3y=2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m\ne-1\\x=\dfrac{m+5}{m+1}\\y=\dfrac{-m+3}{3\left(m+1\right)}\end{matrix}\right.\)
Thay vào pt đầu:
\(\Rightarrow\dfrac{2\left(m+5\right)}{m+1}+\dfrac{\left(m-1\right)\left(-m+3\right)}{3\left(m+1\right)}=4\)
\(\Rightarrow m^2-2m-15=0\Rightarrow\left[{}\begin{matrix}m=-5\\m=3\end{matrix}\right.\)

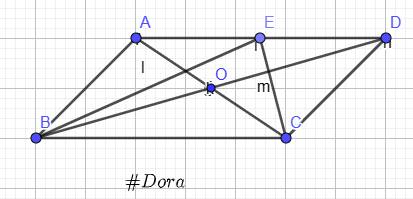
`a)` Vì `O` là trung điểm của `AC;BD`
`=>{(\vec{OA}=-\vec{OC}),(\vec{OB}=-\vec{OD}):}`
Ta có: `\vec{OA}+\vec{OB}+\vec{OC}+\vec{OD}`
`=-\vec{OC}-\vec{OD}+\vec{OC}+\vec{OD}=0`
`b)` Vì `E` là trung điểm `AD=>\vec{EA}=-\vec{ED}`
Ta có: `\vec{EA}+\vec{EB}+2\vec{EC}`
`=\vec{EA}+\vec{EA}+\vec{AB}+2\vec{ED}+2\vec{DC}`
`=-2\vec{ED}+\vec{AB}+2\vec{ED}+2\vec{AB}=3\vec{AB}`
`c)` Ta có: `\vec{EB}+2\vec{EA}+4\vec{ED}`
`=\vec{EB}-2\vec{ED}+4\vec{ED}`
`=\vec{EB}+2\vec{ED}`
`=\vec{EA}+\vec{AB}+2\vec{ED}`
`=-\vec{ED}+\vec{AB}+2\vec{ED}`
`=\vec{AB}+\vec{EC}+\vec{CD}` (Mà `\vec{AB}=-\vec{CD}`)
`=\vec{EC}`
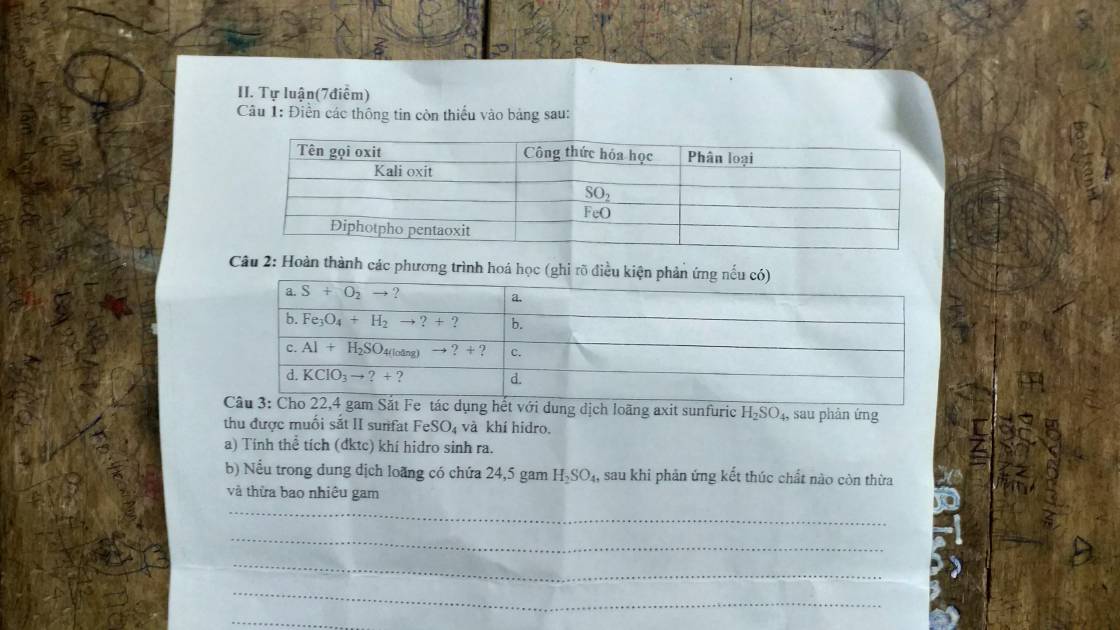
Câu 1:
Kali oxit: K2O: oxit bazo
Lưu huỳnh dioxit: SO2: oxit axit
Sắt (II) oxit: FeO: oxit bazo
Điphotpho pentaoxit: P2O5: oxit axit
Câu 2:
a, \(S+O_2\underrightarrow{t^o}SO_2\)
b, \(Fe_3O_4+4H_2\underrightarrow{t^o}3Fe+4H_2O\)
c, \(2Al+3H_2SO_{4\left(l\right)}\rightarrow Al_2\left(SO_4\right)_3+3H_2\)
d, \(2KClO_3\underrightarrow{t^o,MnO_2}2KCl+3O_2\)