Cho tam giác DEF cân tại D có DH là đường
a)chứng minh tam giác DHF= tam giác DHE
b)Kẻ HC vuông góc DE.HA vuông góc DF. Chứng minh tam giác DCA cân
c)Chứng minh AC//FE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔDEH vuông tại E và ΔDIH vuông tại I có
DH chung
góc EDH=góc IDH
=>ΔDEH=ΔDIH
b: DE=DI
HE=HI
=>DH là trung trực của EI
c: EH=HI
HI<HF
=>EH<HF
d: Xét ΔDFK có
KI,.FE là đường cao
KI cắt FE tại H
=>H là trực tâm
=>DH vuông góc KF

\(\text{#TNam}\)
`a,` Xét Tam giác `HED` và Tam giác `HFD` có
`DE = DF (\text {Tam giác DEF cân tại D})`
\(\widehat{E}=\widehat{F}\) `(\text {Tam giác DEF cân tại D})`
`=> \text {Tam giác HED = Tam giác HDF (ch-gn)}`
`b,` Vì Tam giác `HED =` Tam giác `HFD (a)`
`-> HE = HF (\text {2 cạnh tương ứng})`
Xét Tam giác `HEM` và Tam giác `HFN` có:
`HE = HF (CMT)`
\(\widehat{E}=\widehat{F}\) `(a)`
\(\widehat{EMH}=\widehat{FNH}=90^0\)
`=> \text {Tam giác HEM = Tam giác HFN (ch-gn)}`
`-> EM = FN (\text {2 cạnh tương ứng})`
Ta có: \(\left\{{}\begin{matrix}DE=MD+ME\\DF=ND+NF\end{matrix}\right.\)
Mà `DE = DF, ME = NF`
`-> MD = ND`
Xét Tam giác `DMN: DM = DN (CMT)`
`-> \text {Tam giác DMN cân tại D}`
`->`\(\widehat{DMN}=\widehat{DNM}=\)\(\dfrac{180-\widehat{A}}{2}\)
Tam giác `DEF` cân tại `D`
`->`\(\widehat{E}=\widehat{F}=\)\(\dfrac{180-\widehat{A}}{2}\)
`->`\(\widehat{DMN}=\widehat{E}\)
Mà `2` góc này nằm ở vị trí đồng vị
`-> \text {MN // EF (t/c 2 đt' //)}`

a. lỗi
b. Xét tam giác ABD và tam giác ACD:
AB = AC (tam giác ABC cân tại A)
AD chung
BD = CD ( D là trung điểm BC)
=> tam giác ABD = tam giác ACD (c-c-c)
=> góc BAD = góc CAD (2 góc tương ứng)
Xét tam giác AED và tam giác AFD:
AED = AFD (DE ⊥ AB
DF ⊥ AC)
góc BAD = góc CAD (cmt)
AD chung
=> tam giác AED và tam giác AFD (ch-gn) (đpcm)

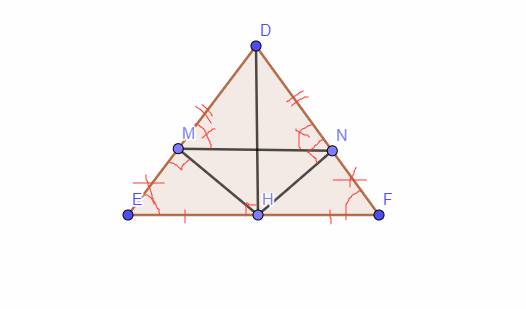
a) xét tam giác DHE và tam giác DHF có
DH chung
DE = DF (gt)
góc DHE = góc DHF (=90 độ)
=> tam giác DHE = tam giác DHF (c.g.c)
=> HE = HF
=> H là trung điểm của EF
b) xét tam giác EMH và tam giác FNH có
HE = HF (cmt)
Góc MEH = góc MFH (gt)
Góc EHM = góc FHM (đối đỉnh)
=> tam giác EMH = tam giác FNH (g.c.g)
=> HM = HN
=> tam giác HMN cân tại H
a: Xét ΔDEH vuông tại H và ΔDFH vuông tại H có
DE=DF
DH chung
=>ΔDEH=ΔDFH
=>EH=FH
=>H là trung điểm của EF
b: Xet ΔDMH và ΔDNH có
DM=DN
góc MDH=góc NDH
DH chung
=>ΔDMH=ΔDNH
=>HM=NH
c: Xet ΔDEF có DM/DE=DN/DF
nên MN//EF
d: ΔDMN cân tại D
mà DI là trug tuyến
nên DI là phân giác của góc EDF
=>D,I,H thẳng hàng

Theo định lí Pytago tam giác DEF vuông tại D
\(DF=\sqrt{EF^2-DE^2}=16cm\)
b, Xét tam giác EDF và tam giác DHF
^DFE _ chung
^EDF = ^DHF = 900
Vậy tam giác EDF ~ tam giác DHF (g.g)
\(\dfrac{EF}{DF}=\dfrac{DF}{HF}\Rightarrow DF^2=EF.HF\)
a: \(DF=\sqrt{20^2-12^2}=16\left(cm\right)\)
b: Xét ΔEDF vuông tại D và ΔDHF vuông tại H có
góc F chung
Do đó: ΔEDF\(\sim\)ΔDHF

a. Xét tam giác ABD và tam giác ACD
AB = AC ( ABC cân )
góc B = góc C ( ABC cân )
AD : cạnh chung
Vậy tam giác ABD = tam giác ACD ( c.g.c )
b. ta có trong tam giác ABC đường trung tuyến cũng là đường cao
=> AD vuông BC
CD = BC : 2 = 12 : 2 =6cm
c.áp dụng định lý pitago vào tam giác vuông ADC
\(AC^2=AD^2+DC^2\)
\(AD=\sqrt{10^2-6^2}=\sqrt{64}=8cm\)
d.Xét tam giác vuông BDE và tam giác vuông CDF có:
AD = CD ( gt )
góc B = góc C
Vậy tam giác vuông BDE = tam giác vuông CDF ( cạnh huyền . góc nhọn)
=> DE = DF ( 2 cạnh tương ứng )
=> tam giác DEF cân tại D
a) Tam giác ABD và tam giác ACD có:
BD = CD (Vì D là trung điểm của BC)
góc B = góc C
(vì tam giác ABC cân tại A)
AB = AC
Do đó: am giác ABD = tam giác ACD (c.g.c)
Suy ra: Góc ADB = góc ADC (cặp góc t/ứng)
b) Vì góc ADB = góc ADC (cmt) mà góc ADB + góc ADC 180 độ (2 góc kề bù)
nên góc ADB = 180 độ / 2 = 90 độ => AD vuông góc với BC
c) Ta có : BD + CD = BC ( Vì D nằm giữa B và C)
mà BC = 12 cm
=> CD = 12 /2 = 6 cm
Vì AD vuông góc với BC nên tam giác ADC vuông tại D
=> AC2AC2 = AD2AD2 +CD2CD2 (Định lý Pytago)
=> 10^2 = AD ^ 2 + 6 ^2
=> AD^2 = 64
=> AD = 8 (cm) (vì AD > 0 )
d) bạn c/m cho tam giác DEB = tam giác DFC (cạnh huyền - góc nhọn) nhé
=> DE = DF (cặp cạnh tương ứng) => tam giác DEF cân tại D( đn)
a: Xét ΔDHF vuông tại H và ΔDHE vuông tại H có
DF=DE
DH chung
=>ΔDHF=ΔDHE
b: Xet ΔDCH vuông tại C và ΔDAH vuông tại A có
DH chung
góc CDH=góc ADH
=>ΔDCH=ΔDAH
=>DC=DA
=>ΔDAC cân tại D
c: Xét ΔDEF có DC/DE=DA/DF
nên AC//EF