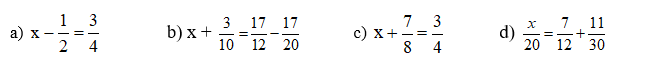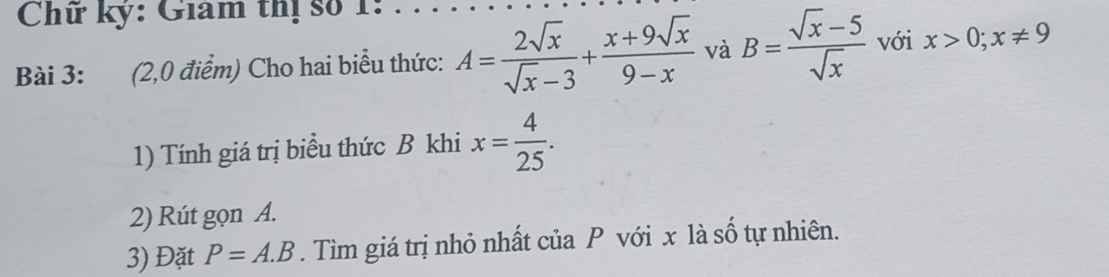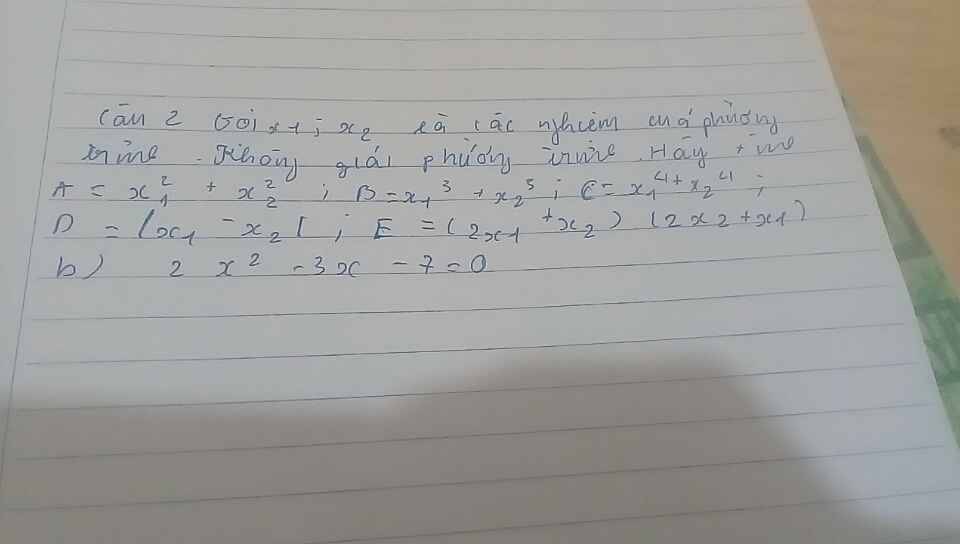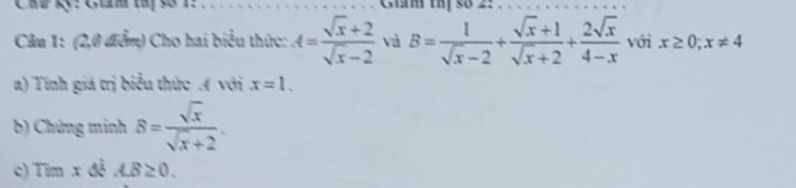
giup em cau nay voi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
24 tháng 3 2023
Đúng(0)
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
28 tháng 2 2022
Lời giải:
a.
$x=\frac{3}{4}+\frac{1}{2}=\frac{5}{4}$
b.
$x+\frac{3}{10}=\frac{17}{12}-\frac{17}{20}=\frac{17}{30}$
$x=\frac{17}{30}-\frac{3}{10}=\frac{4}{15}$
c.
$x=\frac{3}{4}-\frac{7}{8}=\frac{-1}{8}$
d.
$\frac{x}{20}=\frac{7}{12}+\frac{11}{30}=\frac{19}{20}$
$\Rightarrow x=19$
DT
8
H
3 tháng 5 2018
Tổng 2 số: 30*2=60
Số thứ 1: 60/(4+1)*4=48
Số thứ 2: 60-48=12
Vậy St1=48, St2=12
3 tháng 5 2018
Tổng 2 số là :
30 x 2 = 60
Ta có sơ đồ :
St1 :|___|___|___|___| tổng : 60
St2 :|___|
Tổng số phần bằng nhau là :
4 + 1 = 5 (phần)
St1 là :
60 : 5 x 4 = 48
St2 là :
60 - 48 = 12
Đ/S : st1 : 48
st2 : 12
PT
0
KV
7 tháng 4 2023
1) \(B=\dfrac{\sqrt{x}-5}{\sqrt{x}}\)
Thay \(x=\dfrac{4}{25}\) vào B, ta được:
\(B=\dfrac{\sqrt{\dfrac{4}{25}}-5}{\sqrt{\dfrac{4}{25}}}\)
\(=\dfrac{\dfrac{2}{5}-5}{\dfrac{2}{5}}\)
\(=\dfrac{-\dfrac{23}{5}}{\dfrac{2}{5}}\)
\(=-\dfrac{23}{2}\)
2) ĐKXĐ: \(x\ne9;x\ge0\)
\(A=\dfrac{2\sqrt{x}}{\sqrt{x}-3}+\dfrac{x+9\sqrt{x}}{9-x}\)
\(=\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{x+9\sqrt{x}}{x-9}\)
\(=\dfrac{2\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\dfrac{x+9\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{2x+6\sqrt{x}-x-9\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{x-3\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}+3}\)
3) \(P=A.B\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}+3}.\dfrac{\sqrt{x}-5}{\sqrt{x}}\)
\(=\dfrac{\sqrt{x}-5}{\sqrt{x}+3}\)
\(=\dfrac{\sqrt{x}+3-8}{\sqrt{x}+3}\)
\(=1-\dfrac{2}{\sqrt{x}+3}\)
Để P nhỏ nhất thì \(\dfrac{8}{\sqrt{x}+3}\) lớn nhất
Ta có:
\(\dfrac{8}{\sqrt{x}+3}\ge\dfrac{8}{3}\)
\(\Rightarrow P\) nhỏ nhất là \(1-\dfrac{8}{3}=-\dfrac{5}{3}\) khi \(x=0\)
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 1 2023
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{3}{2}\\x_1x_2=-\dfrac{7}{2}\end{matrix}\right.\)
\(A=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=\dfrac{37}{4}\)
\(B=x_1^3+x_2^3=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=\dfrac{153}{8}\)
\(C=x_1^4+x_2^4=\left(x_1^2+x_2^2\right)^2-2\left(x_1x_2\right)^2=\dfrac{977}{16}\)
\(D=\left|x_1-x_2\right|=\sqrt{\left(x_1-x_2\right)^2}=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=\dfrac{\sqrt{65}}{2}\)
\(E=\left(2x_1+x_2\right)\left(2x_2+x_1\right)=2\left(x_1^2+x_2^2\right)+5x_1x_2=1\)