Tính khoảng cách từ điểm M(2,5) đến đường thẳng : 3y + 7 =0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 5 2017
Sử dụng công thức khoảng cách ta có
3. − 2 − 4.1 + 2 3 2 + − 4 2 = m − 2 + 3.1 − 3 m 2 + 3 2
⇔ 8 5 = − 2 m m 2 + 9 ⇔ 8 m 2 + 9 = 10 m ⇔ 64 ( m 2 + 9 ) = 100 m 2 ⇔ 64 m 2 + 576 = 100 m 2 ⇔ 36 m 2 = 576 ⇔ m 2 = 16 ⇔ m = ± 4
Đáp án là phương án C.
Chú ý. Học sinh có thể thử lại các phương án được đưa ra để chọn đáp án đúng, tuy nhiên sẽ tốn nhiều thời gian hơn là làm bài toán trực tiếp.
CM
13 tháng 8 2018
b) Xét tam giác OMB vuông tại O có:
BM2 = OM2 + OB2 = 1 + 1 = 2 ⇒ BM = √2
Tương tự tam giác OAB vuông tại O có:
B A 2 = O A 2 + O B 2 = 1 + 1 = 2 ⇒ BA = 2
Xét tam giác MAB có:
B M 2 + B A 2 = 2 + 2 = 4 = A M 2
⇒ ΔMAB vuông tại B
Do đó, khoảng cách từ M đến đường thẳng (d) là độ dài đoạn BM = 2
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 3 2022
Đường tròn (C) tâm \(I\left(1;-2\right)\) bán kính \(R=\sqrt{5}\)
Điểm M thuộc (C) thỏa mãn khoảng cách từ M tới \(\Delta\) lớn nhất khi M là giao điểm của (C) và đường thẳng d qua I và vuông góc \(\Delta\)
Phương trình d có dạng:
\(2\left(x-1\right)-1\left(y+2\right)=0\Leftrightarrow2x-y-4=0\)
Hệ pt tọa độ giao điểm (C) và d:
\(\left\{{}\begin{matrix}x^2+y^2-2x+4y=0\\y=2x-4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+\left(2x-4\right)^2-2x+4\left(2x-4\right)=0\\y=2x-4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-2x=0\\y=2x-4\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}M\left(0;-4\right)\\M\left(2;0\right)\end{matrix}\right.\)
Với \(M\left(0;-4\right)\Rightarrow d\left(M;\Delta\right)=\dfrac{\left|-2.4+7\right|}{\sqrt{1^2+2^2}}=\dfrac{1}{\sqrt{5}}\)
Với \(M\left(2;0\right)\Rightarrow d\left(M;\Delta\right)=\dfrac{\left|2+0+7\right|}{\sqrt{1^2+2^2}}=\dfrac{9}{\sqrt{5}}\)
Do \(\dfrac{9}{\sqrt{5}}>\dfrac{1}{\sqrt{5}}\) nên \(M\left(2;0\right)\) là điểm cần tìm
PT
1
CM
8 tháng 12 2019
Khoảng cách từ điểm M (-2; 1) đến đường thẳng Δ là:
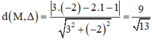
Khoảng cách từ điểm O (0; 0) đến đường thẳng Δ là:
PM
1
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 3 2022
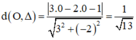
A là giao điểm AB và AC nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}2x+y-5=0\\x-3y+1=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\) \(\Rightarrow A\left(2;1\right)\)
\(d\left(A;...\right)=\dfrac{\left|7.2-8.1+26\right|}{\sqrt{7^2+\left(-8\right)^2}}=\dfrac{32}{\sqrt{113}}\)
CM
2 tháng 12 2018
ĐÁP ÁN C
d ( A ; Δ ) = a . x 0 + b y 0 + c a 2 + b 2 = 3.7 − 4.4 + 8 3 2 + ( − 4 ) 2 = 13 5
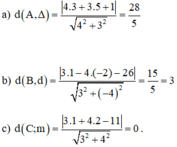
\(d\left(M;3y+7\right)=\dfrac{\left|0.2+3.5+7\right|}{\sqrt{9}}=\dfrac{22}{3}\)