Giải giúp mình với ạ cần gấp ạ 🙏🏻
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



PTHH : 2Al + 6HCl --> 2AlCl3 + 3H2 ↑ (1)
nAlCl3 = \(\dfrac{m}{M}=\dfrac{13,35}{27+35,5.3}=0.1\left(mol\right)\)
Từ (1) => nHCl = 2nH2 = 0.2 (mol)
=> mHCl = n.M = 0.2 x 36.5 = 7.3 (g)
\(PTHH:2Al+6HCl\rightarrow2AlCl_3+3H_2\\ n_{AlCl_3}=\dfrac{m}{M}=\dfrac{13,35}{133,5}=0,1\left(mol\right)\\ Theo.PTHH:n_{HCl}=3.n_{AlCl_3}=3.0,1=0,3\left(mol\right)\\ m_{HCl}=n.M=0,3.36,5=10,95\left(g\right)\)

\(\frac{-6}{30}=\frac{x}{-20}\)
nhân chéo \(x\cdot30=\left(-6\right)\cdot\left(-20\right)\)
=>\(30x=120\)
\(x=4\)
\(\frac{-6}{30}=\frac{3}{y}\)
nhân chéo => \(-6x=90\)
\(x=-15\)
\(\frac{-6}{30}=\frac{z}{5}\)
nhân chéo => \(30z=-30\)
\(z=-1\)
x/-20 = -6/30
=> 30x = 120
<=> x = 4
3/y = -6/30
=> -6y = 90
<=> y = -15
z/5 = -6/30
=> -6z = 150
<=> z = - 25

`@` `\text {Ans}`
`\downarrow`
Độ dài đáy của hình bình hành đó là:
`12 \times 2 = 24 (cm)`
S của hình bình hành đó là:
`12 \times 24 =288 (cm^2)`
Đáp số: `288 cm^2.`
Giải :
Độ dài cạnh đáy là :
12 x 3 = 26 ( m )
Diện tích hình bình hành là :
12 x 36 = 432 ( m2 )
Đ/s :..............

Lời giải:
a. ĐKXĐ: $x>0; x\neq 4$
b.
\(M=\sqrt{x}.\left[\frac{1}{\sqrt{x}-2}+\frac{1}{\sqrt{x}+2}\right].\frac{x-4}{2\sqrt{x}}\)
\(=\frac{2\sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)}.\frac{x-4}{2}=\frac{2\sqrt{x}}{x-4}.\frac{x-4}{2}=\sqrt{x}\)
c. Để $M>3\Leftrightarrow \sqrt{x}>3\Leftrightarrow x>9$
Kết hợp đkxđ suy ra $x>9$ thì $M>3$


\(...=\dfrac{152}{10}-\dfrac{15}{9}+\dfrac{48}{10}-\dfrac{4}{19}=\dfrac{76}{5}-\dfrac{5}{3}+\dfrac{24}{5}-\dfrac{4}{19}\)
\(=\dfrac{76}{5}-\dfrac{5}{3}+\dfrac{24}{5}-\dfrac{4}{19}=\dfrac{76}{5}+\dfrac{24}{5}-\dfrac{5}{3}-\dfrac{4}{19}\)
\(=\dfrac{100}{5}-\dfrac{5}{3}-\dfrac{4}{19}=20-\dfrac{5}{3}-\dfrac{4}{19}=\dfrac{20.57-5.19-4.3}{57}=\dfrac{1033}{57}\)
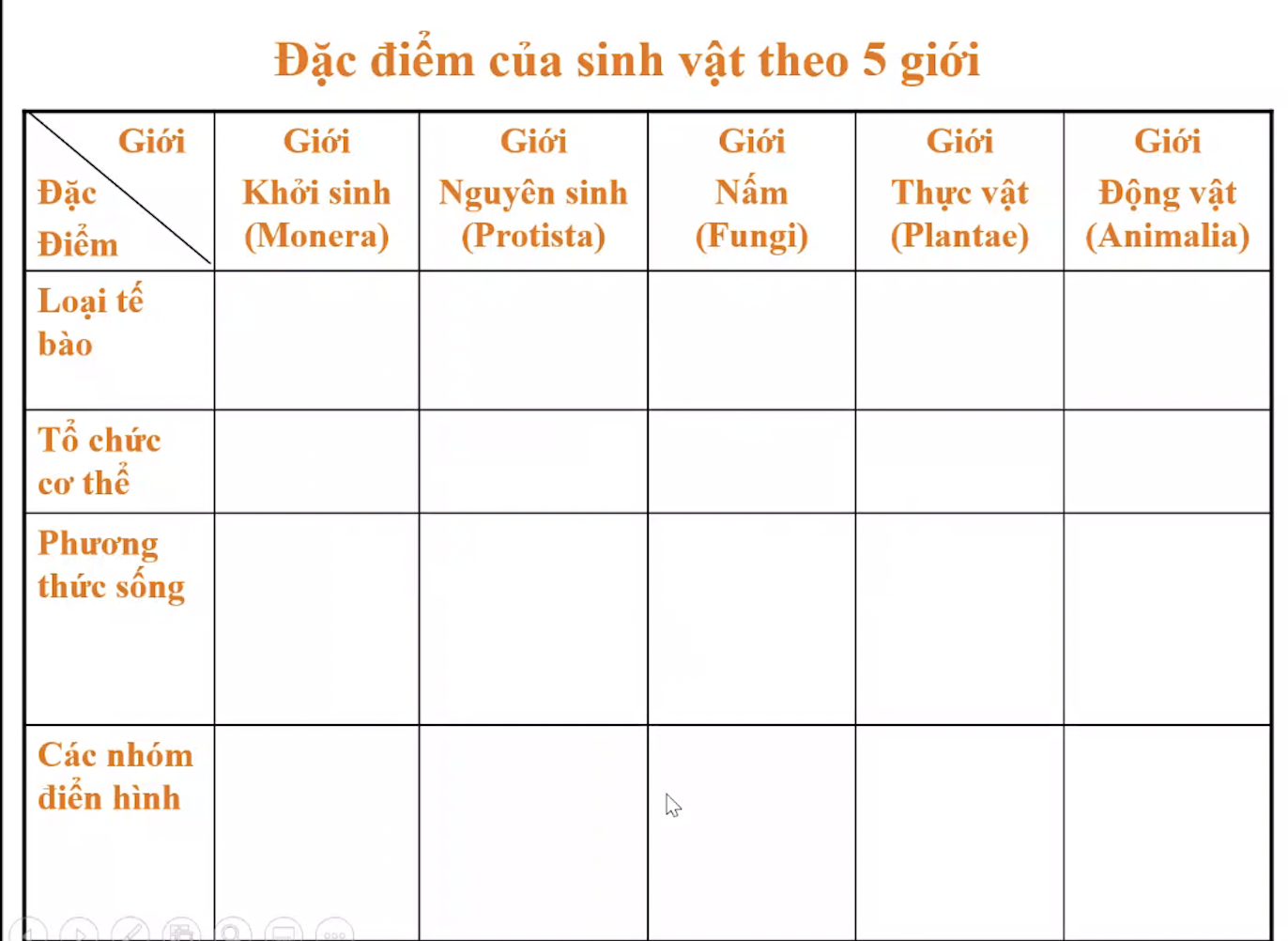 bạn nào giải giúp mình với ạ 🙏🏻
bạn nào giải giúp mình với ạ 🙏🏻

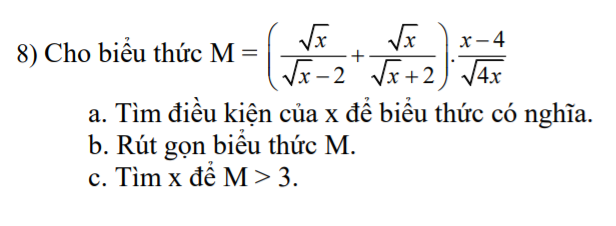

 Mọi người giải giúp mình với ạ mình đang cần gấp ạ, giúp mình nhé
Mọi người giải giúp mình với ạ mình đang cần gấp ạ, giúp mình nhé
1.
Cơ năng ban đầu: \(W=W_đ+W_t=\dfrac{1}{2}mv^2+mgz=\dfrac{1}{2}.4.2^2+4.10.5=208\left(J\right)\)
Cơ năng tại độ cao cực đại:
\(W_{\left(1\right)}=W_{đ\left(1\right)}+W_{t\left(1\right)}\)
\(=\dfrac{1}{2}mv_{\left(1\right)}^2+mgz_{\left(1\right)}\)
\(=mgh_{max}\)
\(=40h_{max}\)
Định luật bảo toàn cơ năng:
\(W=W_{\left(1\right)}\)
\(\Leftrightarrow208=40h_{max}\)
\(\Rightarrow h_{max}=5,2\left(m\right)\)
Vậy độ cao cực đại là \(h_{max}=5,2m\)