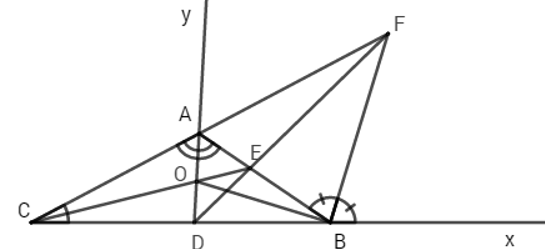
cho tam giác ABC nhọn, các đường phân giác ngoài của góc B và góc C cắt nhau tại I. Đường vuông góc với IA tại A cắt IB, IC lần lượt tại D và E. Chứng minh
a) đường thẳng AI, BE, CD đồng quy tại K
b) điểm K là giao điểm của 3 đường nào của tam giác DIE