Tìm tập hợp các giá trị của m để hàm số y=√ ( m - 2)x^2 - 2( m- 3)x + m - 1 có tập xác định là R
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 6 2021
\(y=\dfrac{x^2-m^2+2m+1}{x-m}\) đúng không nhỉ?
\(y'=\dfrac{x^2-2mx+m^2-2m-1}{\left(x-m\right)^2}\)
Hàm đồng biến trên các khoảng xác định khi và chỉ khi:
\(x^2-2mx+m^2-2m-1\ge0\) ; \(\forall x\)
\(\Leftrightarrow\Delta'=m^2-\left(m^2-2m-1\right)\le0\)
\(\Leftrightarrow m\le-\dfrac{1}{2}\)

NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 7 2021
\(y'=-x^2-2\left(m-2\right)x+m-2\)
Hàm nghịch biến trên TXĐ khi và chỉ khi \(y'\le0;\forall x\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=-1< 0\left(đúng\right)\\\Delta'=\left(m-2\right)^2+m-2\le0\end{matrix}\right.\)
\(\Leftrightarrow\left(m-2\right)\left(m-1\right)\le0\)
\(\Leftrightarrow1\le m\le2\)

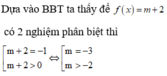
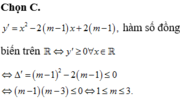
Hàm số xác định \(\Leftrightarrow\left(m-2\right)x^2-2\left(m-3\right)x+m-1\ge0\)
Đặt \(f\left(x\right)=\left(m-2\right)x^2-2\left(m-3\right)x+m-1\ge0\)
\(f\left(x\right)\ge0,\forall x\in R\Leftrightarrow\left\{{}\begin{matrix}a>0\\\Delta\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m-2>0\\\left[-2\left(m-3\right)\right]^2-4\left(m-2\right)\left(m-1\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>2\\4\left(m^2-6m+9\right)-4\left(m^2-3m+2\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow4m^2-24m+36-4m^2+12m-8\le0\)
\(\Leftrightarrow-12m+28\le0\)
\(\Leftrightarrow m\le\dfrac{7}{3}\)
\(KL:m\in(2;\dfrac{7}{3}]\)