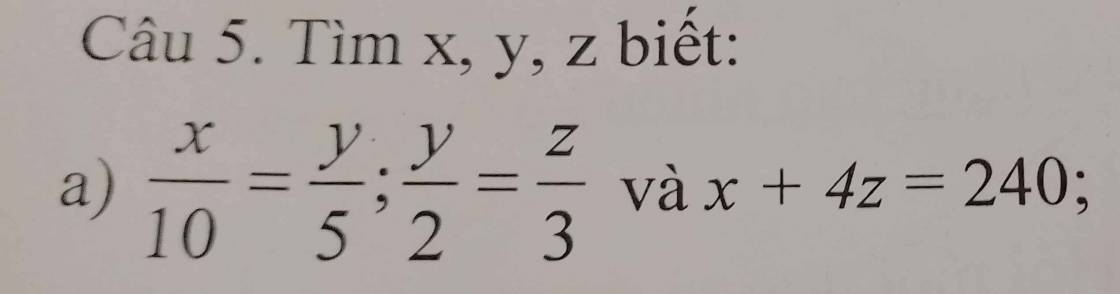 giúp em giải câu này ạ e cần gấp ạ
giúp em giải câu này ạ e cần gấp ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2. There used to have many old buildings 10 years ago
3. I wish a new mall didn't build
4. I have had this wardrobe since my wedding day
5. She hasn't been seen for two years

câu 6: bài học: hãy là chính mình, biết sống hết mình, làm tốt những trách nhiệm, bổn phận của bản thân sẽ được mọi người tôn trọng, yêu quý

Lời giải:
$\frac{x-2y}{3z}$ có thể nhận giá trị lớn nhất nếu $x$ lớn nhất và $y,z$ nhỏ nhất có thể.
$x$ lớn nhất có thể nhận là $14$ (theo điều kiện)
$y,z$ nhỏ nhất có thể nhận là $1,2$ (do $y,z$ phân biệt)
Nếu $x=14, y=1,z=2$ thì $\frac{x-2y}{3z}=2$
Nếu $x=14; y=2, z=1$ thì $\frac{x-2y}{3z}=\frac{10}{3}>2$
Đáp án D.






\(x+\sqrt{4-x^2}=2\)
\(\Leftrightarrow4-x^2=\left(2-x\right)^2\)
\(\Leftrightarrow4-x^2=4-8x+x^2\)
\(\Leftrightarrow4-x^2-4+8x-x^2=0\)
\(\Leftrightarrow8x-2x^2=0\)
\(\Leftrightarrow2x\left(4-x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=0\\4-x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
\(x+\sqrt{1-x^2}=1\)
\(\Leftrightarrow1-x^2=\left(1-x\right)^2\)
\(\Leftrightarrow1-x^2=1-2x+x^2\)
\(\Leftrightarrow1-x^2-1+2x-x^2=0\)
\(\Leftrightarrow2x-2x^2=0\)
\(\Leftrightarrow2x\left(1-x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=0\\1-x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Ta có:
\(\dfrac{x}{10}=\dfrac{y}{5}\)
\(\Rightarrow\dfrac{x}{20}=\dfrac{y}{10}\) \(\left(1\right)\)
\(\dfrac{y}{2}=\dfrac{z}{3}\)
\(\Rightarrow\dfrac{y}{10}=\dfrac{z}{15}\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\)
\(\Rightarrow\dfrac{x}{20}=\dfrac{y}{10}=\dfrac{z}{15}\)
Lại có:
\(\dfrac{z}{15}=\dfrac{4z}{60}\)
Áp dụng tính chất của dãy tỉ số bằng nhau,ta có:
\(\dfrac{x}{20}=\dfrac{y}{10}=\dfrac{4z}{60}=\dfrac{x+4z}{20+60}=\dfrac{240}{80}=3\)
\(\Rightarrow x=3\cdot20=60\)
\(y=3\cdot10=30\)
\(z=3\cdot15=45\)