Cho hàm số \(y=x^2-4x+3\) . Nếu tiếp tuyến của đồ thị hàm số tại điểm M song song với đường thẳng \(-8x+y-2017=0\) thì hoành độ \(x_o\) của M là ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C.
Để thỏa mãn tính chất tiếp tuyến của đồ thị hàm số tại điểm có hoành độ là nghiệm của phương trình y ' ' x = 0 là một đường thẳng song song với trục hoành thì hàm số phải thỏa mãn điều kiện:
Nghiệm của phương trình y ' ' x = 0 là nghiệm của phương trình y ' x = 0 .
Với A: y ' = 3 x 2 − 6 x + 1 ; y ' ' = 6 x − 6 .
y ' ' = 0 ⇔ x = 1 không là nghiệm của phương trình . y ' = 0 Vậy A không thỏa mãn.
Với B: y ' = 3 x 2 − 6 x − 1 ; y ' ' = 6 x − 6 . Tương tự B không thỏa mãn.
Với C: y ' = 3 x 2 − 6 x + 3 ; y ' ' = 6 x − 6 .
y ' ' = 0 ⇔ x = 1 là nghiệm của phương trình y ' = 0 thỏa mãn, vậy ta chọn C.

+Ta có đạo hàm y’ = 3x2- 6mx+ 3( m+ 1) .
Do K thuộc ( C) và có hoành độ bằng -1, suy ra K( -1; -6m-3)
Khi đó tiếp tuyến tại K có phương trình
∆: y= ( 9m+ 6) x+ 3m+ 3
Đường thẳng ∆ song song với đường thẳng d
⇒ 3 x + y = 0 ⇔ y = - 3 x ⇔ 9 m + 6 = - 3 3 m + 3 ≠ 0 ⇔ m = - 1 m ≠ - 1
Vậy không tồn tại m thỏa mãn đầu bài.
Chọn D.

Bài 1:
Đặt: (d): y = (m+5)x + 2m - 10
Để y là hàm số bậc nhất thì: m + 5 # 0 <=> m # -5
Để y là hàm số đồng biến thì: m + 5 > 0 <=> m > -5
(d) đi qua A(2,3) nên ta có:
3 = (m+5).2 + 2m - 10
<=> 2m + 10 + 2m - 10 = 3
<=> 4m = 3
<=> m = 3/4
(d) cắt trục tung tại điểm có tung độ bằng 9 nên ta có:
9 = (m+5).0 + 2m - 10
<=> 2m - 10 = 9
<=> 2m = 19
<=> m = 19/2
(d) đi qua điểm 10 trên trục hoành nên ta có:
0 = (m+5).10 + 2m - 10
<=> 10m + 50 + 2m - 10 = 0
<=> 12m = -40
<=> m = -10/3
(d) // y = 2x - 1 nên ta có:
\(\hept{\begin{cases}m+5=2\\2m-10\ne-1\end{cases}}\) <=> \(\hept{\begin{cases}m=-3\\m\ne\frac{9}{2}\end{cases}}\) <=> \(m=-3\)
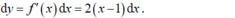


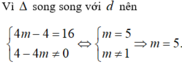
Ủa hỏi mỗi hoành độ thôi hở :D?
\(f'\left(x\right)=2x-4\)
Vi \(pttt//d:y=8x+2017\Rightarrow f'\left(x\right)=8\)
\(\Rightarrow2x-4=8\Leftrightarrow x=6\)