cho đường tròn (c) (x-4)^2+(y-1)^2=9 và delta x-y+5=0. Tìm tọa độ M thuộc delta sao cho từ M kẻ được 2 tiếp tuyến đến đường tròn mà 2 tiếp tuyến đó vuông góc nhau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đường tròn (C) có tâm I (3 ; 3) và có bán kính
\(R = \sqrt {{a^2} + {b^2} - c} = \sqrt {9 + 9 - 14} = 2\)
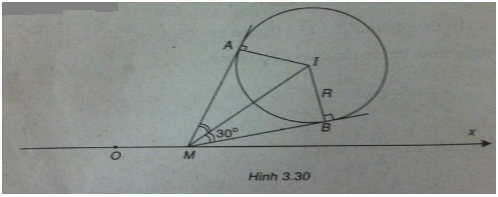
Điểm M(x;0) thuộc Ox.
Từ M kẻ hai tiếp tuyến tiếp xúc với (C) tại A và B. Ta có:
\(\widehat {AMB} = {60^ \circ } \Rightarrow \widehat {IMB} = {30^ \circ }\)
\(\Rightarrow IM = {R \over {\sin {{30}^ \circ }}} = 2R = 4\)
\(IM = 4 \Leftrightarrow \sqrt {{{\left( {x - 3} \right)}^2} + 9} = 4\)
\(\Leftrightarrow {x^2} - 6x + 2 = 0\)
\(\Leftrightarrow x = 3 \pm \sqrt 7\)
Vậy có hai điểm M thỏa mãn đề bài, chúng có tọa độ là :
\({M_1}\left( {3 + \sqrt 7 ;0} \right)\) và \({M_2}\left( {3 - \sqrt 7 ;0} \right)\)

Đáp án A
- Do M thuộc d suy ra M( t; -1-t).
Nếu 2 tiếp tuyến vuông góc với nhau thì MAIB là hình vuông
(A; B là 2 tiếp điểm).
Do đó:
![]()
- Ta có :
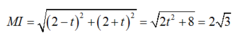
- Do đó : 2t2+ 8= 12
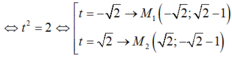
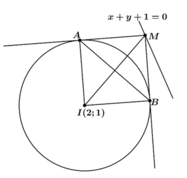

Đường tròn (C) tâm \(I\left(1;3\right)\) bán kính \(R=\sqrt{10}\)
Gọi 2 tiếp điểm là A và B \(\Rightarrow\) tứ giác IAMB là hình chữ nhật (có 3 góc vuông)
Mà \(IA=IB=R\Rightarrow IAMB\) là hình vuông (hcn có 2 cạnh kề bằng nhau)
\(\Rightarrow IM=IA\sqrt{2}=R\sqrt{2}=2\sqrt{5}\)
Gọi \(M\left(3;m\right)\Rightarrow\overrightarrow{IM}=\left(2;m-3\right)\)
\(\Rightarrow IM=\sqrt{4+\left(m-3\right)^2}=2\sqrt{5}\)
\(\Leftrightarrow\left(m-3\right)^2=16\Rightarrow\left[{}\begin{matrix}m=-1\\m=7\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}M\left(3;-1\right)\\M\left(3;7\right)\end{matrix}\right.\)

1: x^2+y^2+6x-2y=0
=>x^2+6x+9+y^2-2y+1=10
=>(x+3)^2+(y-1)^2=10
=>R=căn 10; I(-3;1)
Vì (d1)//(d) nên (d1): x-3y+c=0
Theo đề, ta có: d(I;(d1))=căn 10
=>\(\dfrac{\left|-3\cdot1+1\cdot\left(-3\right)+c\right|}{\sqrt{1^2+\left(-3\right)^2}}=\sqrt{10}\)
=>|c-6|=10
=>c=16 hoặc c=-4
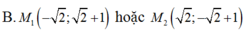
Gọi \(M=\left(m;m+5\right)\left(m\in\right)R\) là điểm cần tìm.
\(\Rightarrow IM=\sqrt{2m^2+32}\)
Ta có: \(cos\left(AM;IM\right)=cos45^o\)
\(\Leftrightarrow\dfrac{R}{IM}=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\dfrac{3}{\sqrt{2m^2+32}}=\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow\) vô nghiệm
Vậy không tồn tại điểm M thỏa mãn yêu cầu bài toán.