Cho tam giác ABC nội tiếp đường tròn (O). D là điểm chính giữa cung AC không chứa B. Ta kẻ dây DE song song với cạnh AB, cắt BC ở I. Chứng tỏ các tam giác ICE và IBD cân
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: góc BAC=góc BCA
=>sđ cung BC=sđ cung BA
b: xy//DE
=>góc AED=góc yAE=góc ABC
c: góc AED=góc ABC
=>góc ABC+góc DEC=180 độ
=>BCDE nội tiếp

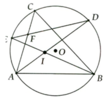
a, B I D ^ = 1 2 s đ D E ⏜ = D B E ^ => ∆BID cân ở D
b, Chứng minh tương tự: DIEC cân tại E, DDIC cân tại D
=> EI = EC và DI = DC
=> DE là trung trực của CI
c, F Î DE nên FI = FC
=> F I C ^ = F C I ^ = I C B ^ => IF//BC

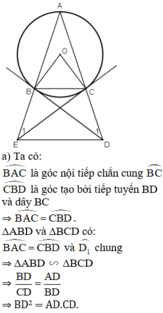
b) ΔABC cân tại A
⇒ AB = AC
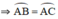
 là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
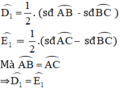
⇒ D và E cùng nhìn BC dưới 1 góc bằng nhau
⇒ BCDE là tứ giác nội tiếp.
c. Tứ giác BCDE nội tiếp

⇒ BC // DE (hai góc đồng vị bằng nhau).

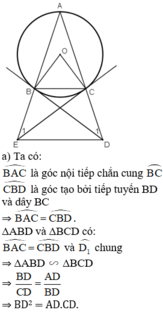
b) ΔABC cân tại A
⇒ AB = AC
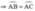
 là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
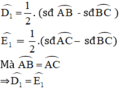
⇒ D và E cùng nhìn BC dưới 1 góc bằng nhau
⇒ BCDE là tứ giác nội tiếp.
c. Tứ giác BCDE nội tiếp

⇒ BC // DE (hai góc đồng vị bằng nhau).
DE//AB
=>sđ cung AD=sđ cung BE=sđ cung CD=1/2*sđ cung AC
góc BIE=1/2(sđ cung BE+sđ cung CD)
=1/2*(sđ cung CD+sđ cung CD)
=sđ cung CD
=2*góc CEI
=>ΔIEC cân tại I
=>IE=IC
Xét ΔIBE và ΔIDC có
góc BIE=góc DIC
IE=IC
góc IEB=góc ICD
=>ΔIBE=ΔIDC
=>IB=ID
=>ΔIBD cân tại I