hãy chia số 786 thành những phần tỉ lệ nghịch với các số 0,2 , \(3\dfrac{1}{3}\) , \(\dfrac{4}{5}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
2
NM
0
CB
0
KZ
1
TC
8 tháng 12 2018
Gọi 3 phần số 786 chia ra là a,b,c
Áp dung Tc của dãy tỉ số bằng nhau , ta có:
\(\frac{a}{0.2}=\frac{b}{3\frac{1}{3}}=\frac{c}{\frac{4}{5}}=\frac{a+b+c}{0.2+3\frac{1}{3}+\frac{4}{5}}=\frac{786}{\frac{13}{3}}\)
HT
3
19 tháng 8 2015
dùng tỉ lệ thức:
Gọi 3 phần đó là: a,b,c
rùi tính từ từ...
........
16 tháng 9 2018
Giải: gọi 3 phần cần chia là a,b,c
ta có a+b+c=786
vì a,b,c TLN với 3,4,5 nên ta có
3a=4b=5c <=>3a trên 60= 4b trên 60 = 5c trên 60
<=> a trên 20= b trên 15 = c trên 12
ad tc dãy tỉ số bàng nhau ta có
bạn hãy tự làm phàn này dễ
ML
2
G
3 tháng 3 2018
Ta có: \(0,2=\frac{1}{5};3\frac{1}{3}=\frac{10}{3}\)
Ta có: Gọi 3 phần đó là \(a;b;c\) ta có: \(\frac{a}{\frac{1}{5}}=\frac{b}{\frac{10}{3}}=\frac{c}{\frac{4}{5}}\Leftrightarrow5a=\frac{3b}{10}=\frac{5c}{4}\)
\(\Rightarrow\frac{5a}{15}=\frac{3b}{150}=\frac{5c}{60}\Leftrightarrow\frac{a}{3}=\frac{b}{50}=\frac{c}{12}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có: \(\frac{a}{3}=\frac{b}{50}=\frac{c}{12}=\frac{a+b+c}{3+50+12}=\frac{786}{65}\)
Nhân ra là ra a;b;c
1 tháng 3 2020
a, Gọi 3 phần đó là \(x,y,z\)
Ta có: \(\frac{x}{\frac{1}{3}}=\frac{y}{\frac{1}{5}}=\frac{z}{\frac{1}{6}}\)và \(x+y+z=315\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{x}{\frac{1}{3}}=\frac{y}{\frac{1}{5}}=\frac{z}{\frac{1}{6}}=\frac{x+y+z}{\frac{1}{3}+\frac{1}{5}+\frac{1}{6}}=\frac{315}{0,7}=450\)
\(\frac{x}{\frac{1}{3}}=450\Leftrightarrow x=150\)
\(\frac{y}{\frac{1}{5}}=450\Leftrightarrow y=90\)
\(\frac{z}{\frac{1}{6}}=450\Leftrightarrow z=75\)
Vậy 3 phần đó là \(150;90;75\)
Mình làm hơi tắt, bạn thông cảm nhé!
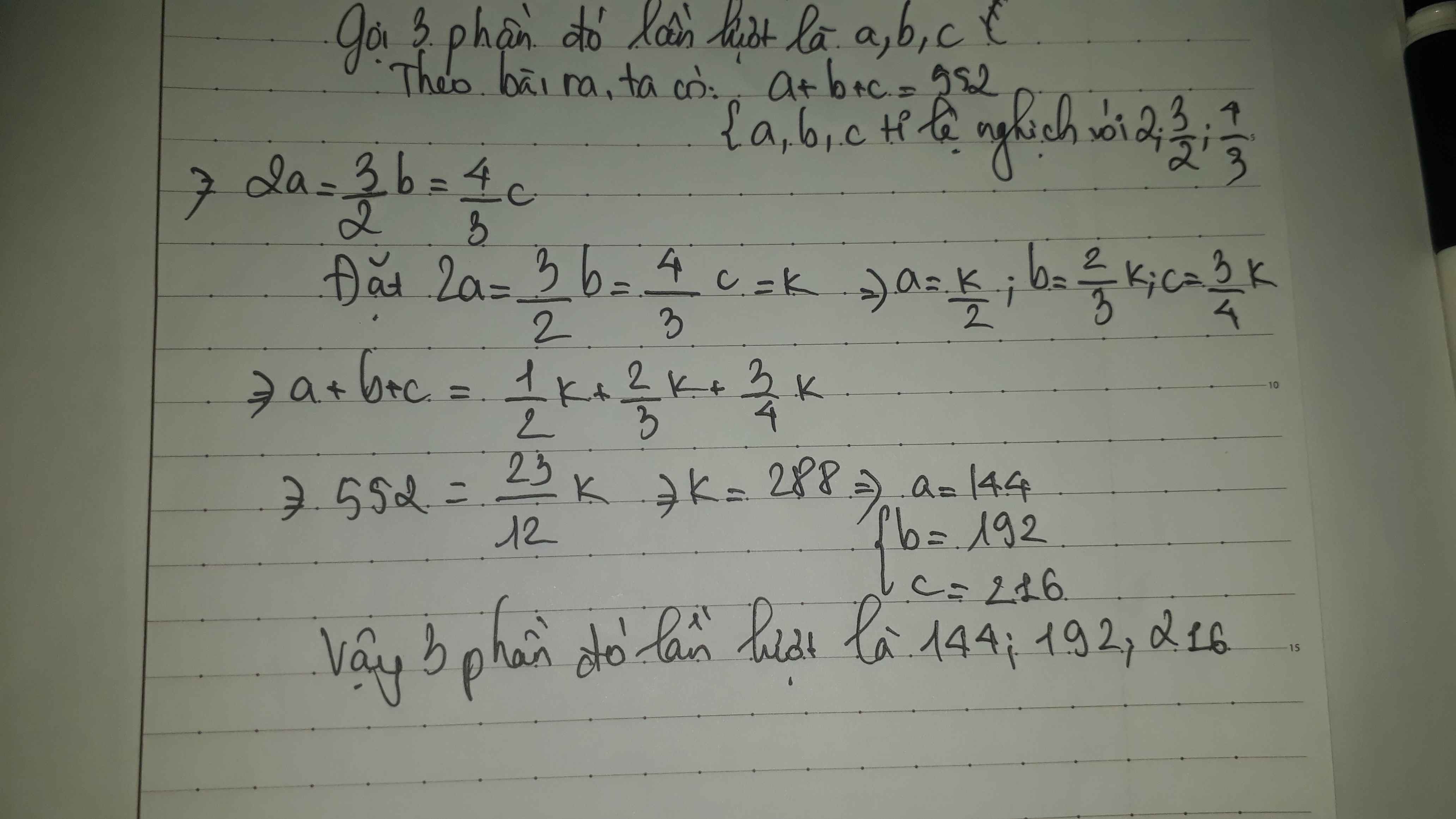
Gọi ba phần cần tìm lần lượt là a,b,c
Theo đề, ta có: \(\dfrac{1}{5}a=\dfrac{10}{3}b=\dfrac{4}{5}c\)
=>\(\dfrac{a}{5}=\dfrac{b}{\dfrac{5}{4}}=\dfrac{c}{\dfrac{3}{10}}\)
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{a}{5}=\dfrac{b}{\dfrac{5}{4}}=\dfrac{c}{\dfrac{3}{10}}=\dfrac{a+b+c}{5+\dfrac{5}{4}+\dfrac{3}{10}}=\dfrac{786}{\dfrac{131}{20}}=120\)
=>a=600; b=150; c=36